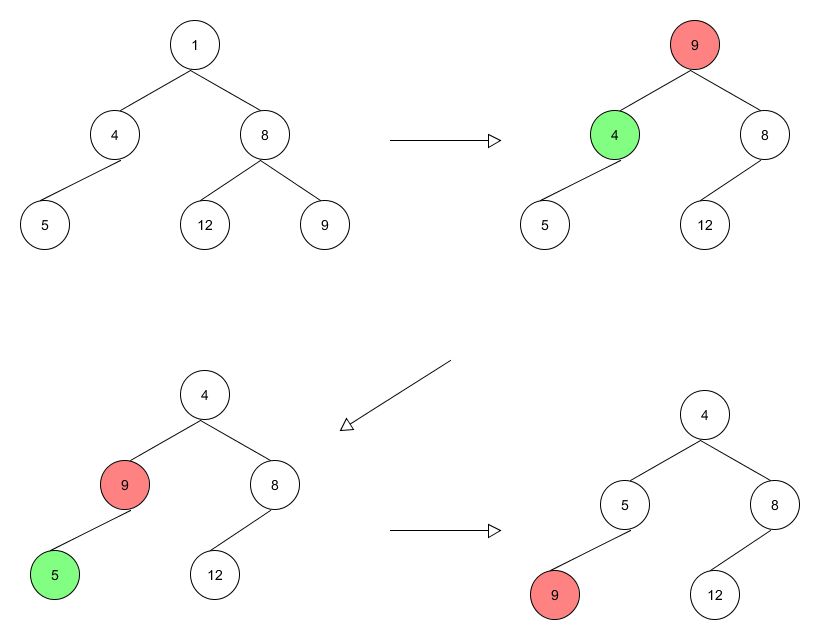
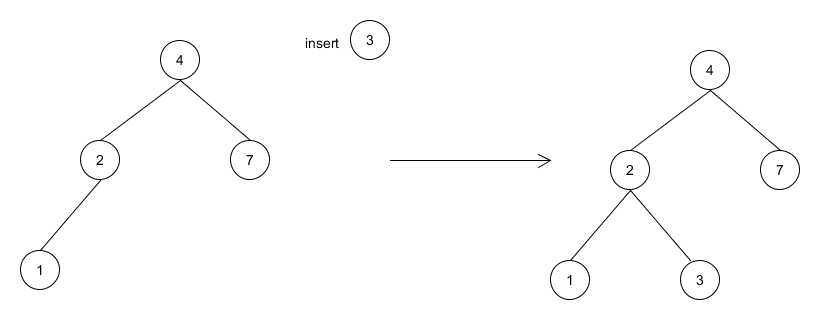
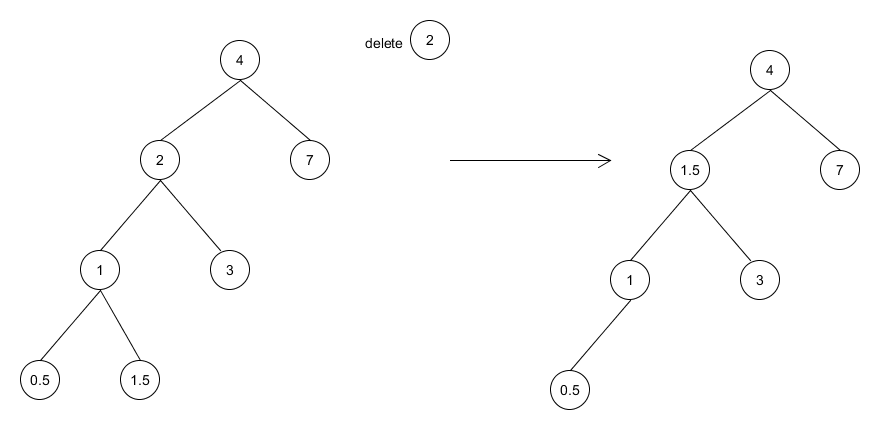
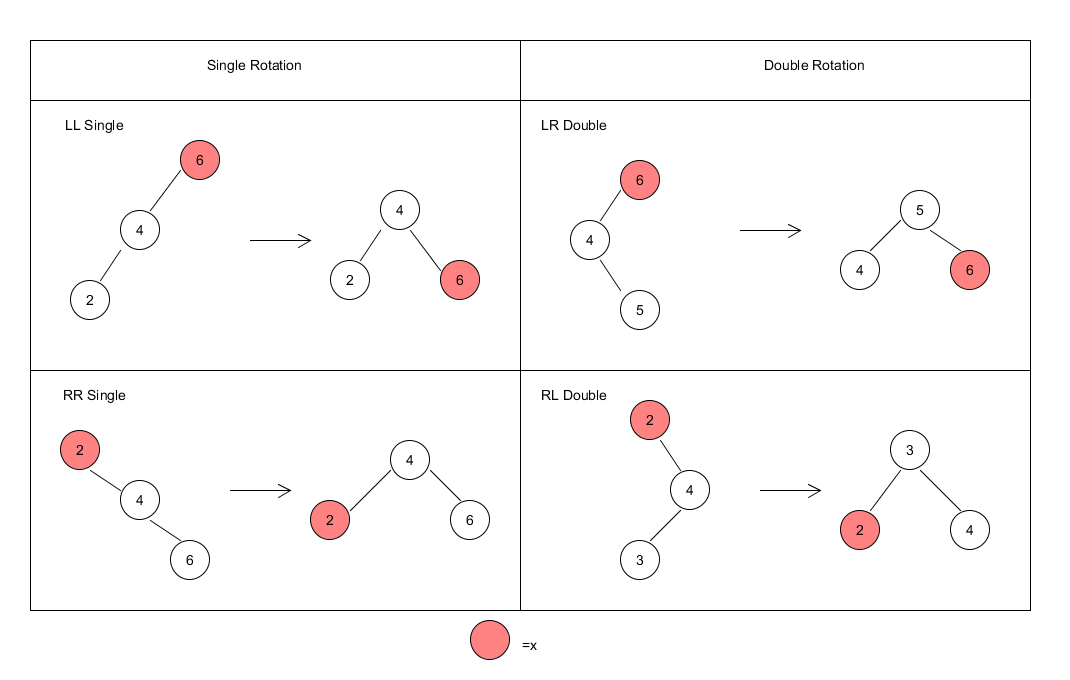
有尽小数在实数系中处处稠密
定理 设$a$和$b$是实数, $a<b$. 则存在有尽小数$c$, 满足
$$
a < c < b
$$
确界原理
$\mathbb{R}$的任何非空而有上界的子集合$D$在$\mathbb{R}$中有上确界.
常用不等式
绝对值不等式
$$
|a+b| \le |a| + |b| \\
||a|-|b|| \le |a - b| \\
$$
Bernoulli不等式
$$
(1+x)^n \ge 1+nx
$$
均值不等式
$$
\frac{x_1+x_2}{2} \ge \sqrt{x_1x_2}
$$
AM-GM不等式
定理 设$x_1,x_2,\cdots,x_n \ge 0$, 则以下的算术平均数与几何平均数不等式成立:
$$
\frac{x_1+x_2+\cdots+x_n}{n} \ge \sqrt[n]{x_1x_2 \cdots x_n}
$$
三角函数不等式
定理 对于用弧度表示的角$x$, 有以下不等式成立
$$
\forall x \in (0, \frac{\pi}{2}) \qquad \sin x < x < \tan x
$$
有界序列, 无穷小序列, 收敛序列性质一览
- 两个有界序列的和是有界序列, 两个有界序列的积是有界序列.
- 两个无穷小序列的和是无穷小序列, 两个无穷小序列的积也是无穷小序列.
- 无穷小序列和有界序列的积是有界序列.
- $\{a_n\}$是无穷小序列当且仅当$\{|a_n|\}$是无穷小序列.
- 实数与无穷小序列的积是无穷小序列.
- 有限个无穷小序列的和和积都是无穷小序列.
- 收敛序列是有界序列.
- $\lim |x_n| = |\lim x_n|$.
- $\lim (x_n \pm y_n) = \lim x_n \pm \lim y_n$.
- $\lim (x_ny_n) = \lim x_n \cdot \lim y_n$.
- 若$x_n \ne 0$且$\lim x_n \ne 0$, $\lim \frac{1}{x_n} = \frac{1}{\lim x_n}$.
- $\lim(cx_n) = c\lim x_n$.
- 若$x_n \ne 0$且$\lim x_n \ne 0$, $\lim \frac{y_n}{x_n} = \frac{\lim y_n}{\lim x_n}$.
序列收敛原理
- 单调有界序列收敛.
- 有界序列具有收敛的子序列.
- 基本序列收敛.
函数极限定义
定义I(序列式定义)
设$a, A \in \bar{\mathbb{R}}$, 并设函数$f(x)$在$a$点的某个去心邻域$U^*(a)$上有定义. 如果对于任何满足条件$x_n \rightarrow a$的序列$\{x_n\} \subset U^*(a)$, 相应的函数值序列$\{f(x_n)\}$都以$A$为极限,那么我们就说当$x \rightarrow a$时, 函数$f(x)$的极限为$A$, 记为
$$
\lim_{x \rightarrow a}f(x) = A
$$
定义II($\epsilon\text{-}\delta$式定义)
设$a, A \in \mathbb{R}$, 并设函数$f(x)$在$a$点的某个去心邻域$U^*(a,\eta)$上有定义. 如果对任意的$\epsilon > 0$, 存在$\delta > 0$, 使得只要$0 < |x - a| < \delta$, 就有
$$
|f(x) - A| < \epsilon
$$
那么我们就说: $x \rightarrow a$时函数$f(x)$的极限是$A$, 记为
$$
\lim_{x \rightarrow a}f(x) = A
$$
*定义II仅定义了自变量和因变量都是实数的情况, 除此之外还有$a = \pm\infty$, $A = \pm\infty$与实数进行组合的多种情况, 在此不一一列举.
连续函数重要性质
定理1 连续点附近有界.
定理2 两个函数$f(x)$, $g(x)$在$x_0$点连续, 有
- $f(x) \pm g(x)$在$x_0$处连续.
- $f(x)g(x)$在$x_0$处连续.
- $\frac{f(x)}{g(x)}$在使得$g(x_0) \ne 0$的$x_0$处连续.
- $|f(x)|$在$x_0$处连续.
- 若$f(x_0) < g(x_0)$, 则存在$\delta > 0$使得对于$x \in U(x_0, \delta)$有$f(x) < g(x)$.
定理3(复合函数连续性) 设函数$f(x)$在$x_0$处连续, 函数$g(x)$在$y_0=f(x_0)$处连续, 则复合函数$g \circ f(x) = g(f(x))$在$x_0$处连续.
定理4(介值定理)
设函数$f$在闭区间$[a,b]$连续. 对于任意$\gamma$满足$f(a) < \gamma < f(b)$或$f(a) > \gamma > f(b)$, 存在$c \in (a,b)$使得
$$
f(c) = \gamma
$$
定理5 在闭区间$[a,b]$连续的函数$f$在$[a,b]$上有界.
定理6(最大值与最小值定理) 设函数$f$在闭区间$[a,b]$上连续, $M,m$分别是该函数的上确界和下确界, 则存在$x’, x’’ \in [a,b]$使得
$$
f(x’) = M, \quad f(x’’) = m
$$
定理7(一致连续性定理) 在闭区间$[a,b]$上连续的函数$f$在$[a,b]$上一致连续.
无穷量
设函数$\phi(x)$和$\psi(x)$在$a$点的某个取心邻域$U^*(a)$上有定义, 并设在$U^*(a)$上$\phi(x) \ne 0$. 我们分别用记号$O$, $o$与$\sim$表示比值$\frac{\psi(x)}{\phi(x)}$在$a$点邻近的几种情况:
- $\psi(x)=O(\phi(x))$表示$\frac{\psi(x)}{\phi(x)}$是$x\rightarrow a$时的有界变量.
- $\psi(x)=o(\phi(x))$表示$\frac{\psi(x)}{\phi(x)}$是$x\rightarrow a$时的无穷小量.
- $\psi(x)\sim \phi(x)$表示$\lim_{x\rightarrow a}\frac{\psi(x)}{\phi(x)} = 1$.
重要极限小记
$$
\begin{eqnarray}
\lim_{x\rightarrow 0}&\frac{\sin x}{x} &= 1 \\
\lim_{x\rightarrow \infty}&(1+\frac{1}{x})^x &= e \\
\lim_{\alpha \rightarrow 0}&\frac{\ln(1+\alpha)}{\alpha} &= 1 \\
\lim_{\alpha \rightarrow 0}&\frac{\log_b(1+\alpha)}{\alpha} &= \frac{1}{\ln b} \\
\lim_{\alpha \rightarrow 0}&\frac{e^\alpha-1}{\alpha} &= 1 \\
\lim_{\alpha \rightarrow 0}&\frac{(1+\alpha)^\mu - 1}{\alpha} &= \mu \\
\end{eqnarray}
$$
基础微分
导数 设函数$f(x)$在$x_0$点邻近有定义. 如果存在有穷极限
$$
\lim_{\Delta x \rightarrow 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}
$$
那么我们就说函数$f(x)$在$x_0$点可导, 并把上述极限值称为$f(x)$在$x_0$点的导数, 记为$f’(x_0)$(Lagrange)或$\frac{df(x_0)}{dx}$(Leibnitz).
微分 设函数$f(x)$在$x$点邻近有定义, 如果
$$
f(x+h)-f(x)=Ah + o(h)
$$
其中$A$与$h$无关, 那么我们就说函数$f$在$x$点可微.
设函数$y=f(x)$在$x_0$处可微, 引入记号
$$
\begin{align}
dx &:= \Delta x \nonumber \\
dy &:= f’(x_0)dx = f’(x_0)\Delta x \nonumber
\end{align}
$$
$dy$叫做函数$y=f(x)$在$x_0$点的微分.
初等函数导数表
| 函数 | 导数 | 备注 |
|---|---|---|
| $C$ | $0$ | |
| $x^m$ | $mx^{m-1}$ | $m \in \mathbb{N}_+$ |
| $x^{-m}$ | $-mx^{-m-1}$ | $m \in \mathbb{N}_+, \quad m \ne 0$ |
| $x^\mu$ | $\mu x^{\mu-1}$ | $\mu \in \mathbb{R}, \quad x > 0$ |
| $\sin x$ | $\cos x$ | |
| $\cos x$ | $-\sin x$ | |
| $\tan x$ | $\frac{1}{\cos^2 x}$ | $x \ne k\pi + \frac{\pi}{2}$ |
| $\cot x$ | $-\frac{1}{\sin^2 x}$ | $x \ne k\pi$ |
| $\arcsin x$ | $\frac{1}{\sqrt{1-x^2}}$ | $|x| < 1$ |
| $\arccos x$ | $-\frac{1}{\sqrt{1-x^2}}$ | $|x| < 1$ |
| $\arctan x$ | $\frac{1}{1+x^2}$ | |
| $\text{arccot }x$ | $-\frac{1}{1+x^2}$ | |
| $e^x$ | $e^x$ | |
| $a^x$ | $a^x\ln a$ | $a>0$ |
| $\ln x$ | $\frac{1}{x}$ | $x>0$ |
| $\log_a x$ | $\frac{1}{x} \log_a e$ | $a>0, \quad x>0$ |
不定积分
设函数$f$在区间$I$上有定义, 函数$F$是$f$的一个原函数, 则函数簇
$$
F(x) + C (C \in \mathbb{R})
$$
表示$f$的一切原函数. 我们把这函数簇叫做函数$f(x)$的不定积分, 或者叫做微分形式$f(x)dx$的不定积分, 记为
$$
\int f(x)dx = F(x) + C
$$
不定积分表
| 不定积分表 |
|---|
| $\int 0 dx = C$ |
| $\int 1 dx = x + C$ |
| $\int x^\mu dx = \frac{1}{\mu + 1} x^{\mu+1} + C (\mu \ne -1)$ |
| $\int x^{-1} dx = \int \frac{dx}{x} = \ln{|x|} + C$ |
| $\int \frac{dx}{x-a} = \ln{|x-a|} + C$ |
| $\int e^x dx = e^x + C$ |
| $\int a^x dx = \frac{a^x}{\ln{a}}+C(a > 0, a \ne 1)$ |
| $\int \cos x dx = \sin x + C$ |
| $\int \sin x dx = -\cos x + C$ |
| $\int \frac{dx}{\cos^2 x} = \tan x + C$ |
| $\int \frac{dx}{\sin^2 x} = - \cot x + C$ |
| $\int \frac{dx}{1+x^2} = \arctan x + C$ |
| $\int \frac{dx}{\sqrt{1-x^2}} = \arcsin x + C$ |
| $\int \frac{dx}{\sqrt{x^2 \pm a^2}} = \ln{|x+\sqrt{x^2 \pm a^2} |} + C$ |
定积分
设函数$f$在区间$[a,b]$有定义. 如果存在实数$I$, 使得对于任意无穷细分割序列${P^{(n)}}$, 不论相应于每个分割$P^{(n)}$的标志点组$\xi^{(n)}$怎样选择, 都有
$$
\lim_{n \rightarrow +\infty} \sigma(f, P^{(n)}, \xi^{(n)})=I
$$
那么我们就说函数$f$在$[a,b]$上可积,并把$I$称为函数$f$在$[a,b]$上的定积分,记为
$$
\int_a^bf(x)dx = \lim_{|P| \rightarrow 0}\sigma(f,P,\xi)=I
$$
牛顿-莱布尼茨公式
设函数$f$在闭区间$[a,b]$连续. 如果存在函数$F$在$[a,b]$连续, 在$(a,b)$可导, 并且满足
$$
F’(x) = f(x), \forall x \in (a,b)
$$
那么函数$f$在$[a,b]$上可积,并且
$$
\int_a^bf(x)dx=F(b)-F(a)
$$
二重积分的计算
设函数$z = f(x,y)$在闭区间$D$上连续, 其中$D$由直线$x=a, x=b (a < b)$及曲线$y=\varphi_1(x), y=\varphi_2(x) (\varphi_1(x) \le \varphi_2(x), a \le x \le b)$围成. 这时$f(x,y)$的二重积分可表示成如下的累次积分
$$
\iint f(x,y)d\sigma = \int_a^b [\int_{\varphi_1(x)}^{\varphi_2(x)} f(x,y)dy]dx
$$
基础微分方程
本记将基础微分方程分为5种类型,分别是可分离变量型、齐次型、一阶线性型、二阶可降阶型和二阶线性常系数微分方程。
可分离变量型
形如
$$
\frac{dy}{dx} = g(x)h(y)
$$
的方程, 可将其变换为
$$
\frac{dy}{h(y)} = g(x)dx
$$
并在两边同时积分.
齐次型
形如
$$
\frac{dy}{dx} = f(\frac{y}{x})
$$
的方程, 可令$u = \frac{y}{x}$代入得到
$$
\frac{xdu}{dx} + u = f(u)
$$
并可进行变量分离得到
$$
\frac{du}{f(u)-u} = \frac{dx}{x}
$$
一阶线性型
形如
$$
y’ + p(x)y = q(x)
$$
的方程, 两边同时乘以$e^{\int p(x)dx}$可得
$$
\begin{align*}
&e^{\int p(x)dx}y’ + e^{\int p(x)dx}p(x)y = e^{\int p(x)dx}q(x) \\
\Rightarrow& [e^{\int p(x)dx}y]' = e^{\int p(x)dx}q(x) \\
\Rightarrow& y = e^{-\int p(x)dx}[\int e^{\int p(x)dx}q(x)dx + C_1]
\end{align*}
$$
二阶可降阶型
形如
$$
y’’ = f(x, y’)
$$
或
$$
y’’ = f(y’, y)
$$
的方程, 可令$y’ = p$, 则$y’’ = \frac{dp}{dx} = \frac{dp}{dy}p$, 并化为一阶方程.
二阶线性常系数微分方程
形如
$$
y’’ + py’ + qy = f(x)
$$
的方程, 考察其特征方程
$$
\lambda^2 + p\lambda + q = 0
$$
其齐次型($f(x)=0$)的通解如下表所示
| 特征根 | 通解 |
|---|---|
| $\lambda_1, \lambda_2 \in \mathbb{R}, \lambda_1 \ne \lambda_2$ | $y = C_1e^{\lambda_1x}+C_2e^{\lambda_2x}$ |
| $\lambda_1, \lambda_2 \in \mathbb{R}, \lambda_1 = \lambda_2$ | $y=(C_1+C_2x)e^{\lambda_1x}$ |
| $\lambda_{1,2}=\alpha \pm i\beta$ | $y=e^{ax}(C_1\cos \beta x + C_2 \sin \beta x)$ |
其非齐次型的特解如下表所示
| $f(x)$形式 | 条件 | 特解 |
|---|---|---|
| $\alpha \ne \lambda_1, \alpha \ne \lambda_2$ | $y^* = e^{\alpha x}Q_n(x)$ | |
| $P_n(x)e^{\alpha x}$ | $\alpha = \lambda_1$ 或 $\alpha = \lambda_2$ | $y^* = xe^{\alpha x}Q_n(x)$ |
| $\alpha = \lambda_1 = \lambda_2$ | $y^* = x^2e^{\alpha x}Q_n(x)$ | |
| $e^{\alpha x}[P_n(x)\cos \beta x + P_m(x)\sin \beta x](\beta \ne 0)$ | $\lambda \ne \alpha \pm i\beta$ | $y^* = e^{\alpha x}[Q_l(x)\cos \beta x + R_l(x)\sin \beta x]$ |
| $\lambda = \alpha \pm i\beta$ | $y^* = xe^{\alpha x}[Q_l(x)\cos \beta x + R_l(x)\sin \beta x]$ |
其中, $P_n(x)$为关于$x$的$n$次多项式, $l = \max\{n, m\}$.
参考文献
张筑生. 数学分析新讲. 北京大学出版社.