概览
给定一个整数n,求所有小于等于n的非负整数中数字1的个数之和。
暴力求解(TLE)
本题可使用暴力求解枚举每一个小于等于n的非负整数,虽然C语言给定的参数是int,但穷举依然会超时。
时间复杂度:$O(n)$
空间复杂度:$O(1)$
动态规划
标答中给出了一种基于数学的方法,但本题依然可使用动态规划的思想求解。
状态设计:
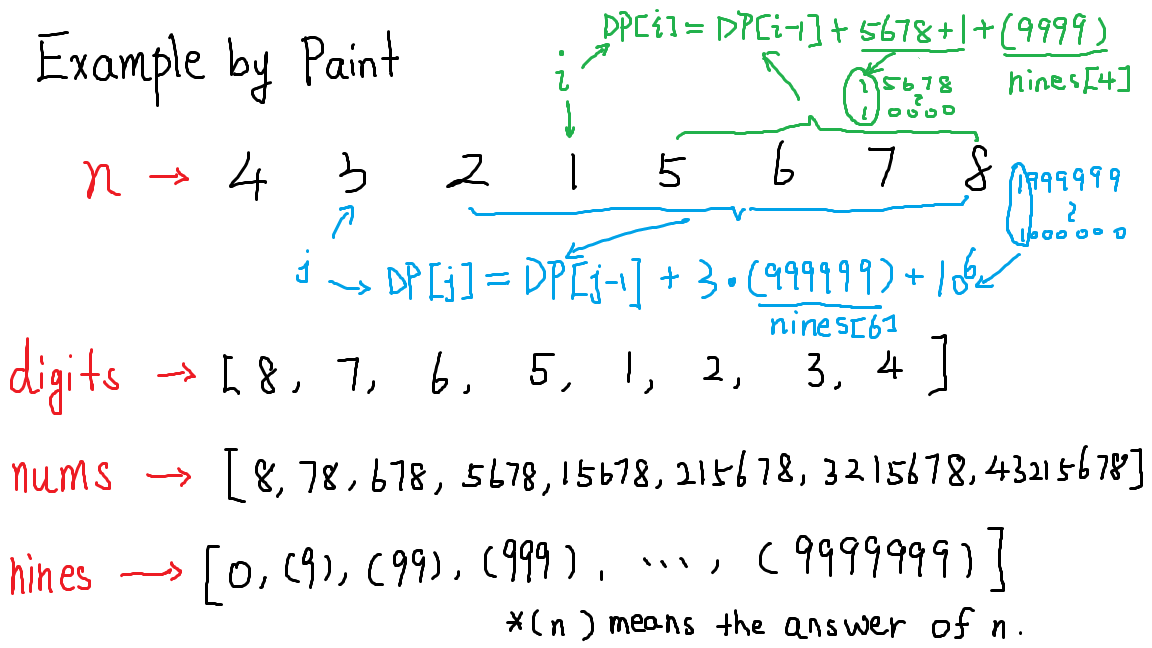
令DP[i]表示前i位数的答案。
状态转移:
这样的状态设计可以使复杂度降至$O(d)$,$d$表示n的位数,但是状态转移过程不单单涉及到前一状态,还涉及到一些已知的结论。
令digits[i]表示第i + 1个数字,nums[i]表示前i + 1位数组成的数字(i低到高,i = 0, 1, 2, ..., d - 1),nines[i]表示i个9组成的数字的答案,则有
nines[i] = nines[i - 1] * 10 + pow(10, i - 1);- 当
digits[i] == 0时,DP[i] = DP[i - 1]; - 当
digits[i] == 1时,DP[i] = DP[i - 1] + nums[i - 1] + 1 + nines[i]; - 当
digits[i] > 1时,DP[i] = DP[i - 1] + nines[i] * digits[i] + pow(10, i)。
具体来说,一个位数为$d$的数$n$可以做如下分解:
$$
n = n_{(d)} * 10^{d - 1} + n’
$$
其中$n’$表示去除最高位所得的数,$n_{(i)}$为整数$n$第$i$位的数字。在算法中DP[i - 1]即表达了数$n’$对应的答案,剩余部分可分为三种情况:
- $n_{(d)} = 0$,这种情况只会不会出现在最高位,直接相等即可。
- $n_{(d)} = 1$,则对于任意$0 \le k \le n’$,首位的1都会计算一次次数,这部分的次数为
nums[i - 1] + 1次;同时,$10^{d - 1}$的部分则为$d - 1$个$9$组成的数字的答案。 - $n_{(d)} > 1$,则$n_{(d)} * 10^{d - 1}$的部分包括$n_{(d)}$个$d - 1$个$9$组成的数字的答案以及经过第$d$位为1时数字的个数共$10^{d - 1}$个。
综上所述,算法的时间复杂度为$O(d)$,空间复杂度为$O(d)$,其中$d$为数字的位数。