Capacitated Facility Location Problem

Posted on | Edited on

Capacitated Facility Location Problem(CFLP)问题是一个典型的NP-Hard问题，该问题的描述如下，

  • 给定N个设施(facility)和M位顾客(customer)，每个设施有一个最大容量s，并且可以选择开启或关闭，开启有一个开启费用f。
  • 每位顾客有一个需求d，需要被某个或某些个设施满足，某个设施满足的需求数不得超过其最大容量s。
  • 每个设施到每个顾客都有一个满足费用c，即满足某个顾客单位需求的费用。
  • 最小化满足所有顾客所有需求的总费用。

分析

引入如下的数学符号，

  • $N$表示设施数，$M$表示顾客数。
  • $s_i, \forall i = 0,…,N-1$表示设施$i$的最大容量。
  • $f_i, \forall i = 0,…,N-1$表示设施$i$的开启费用。
  • $d_i, \forall i = 0,…,M-1$表示顾客$i$的需求。
  • $c_{ij}, \forall i = 0,…,N-1, j = 0,…,M-1$表示设施$i$满足顾客$j$单位需求所需费用。
  • 注：一般而言，用$c_{ij}$表示的是满足顾客所有需求所需费用，这里为避免引入除法和分数采用单位需求。

并将CFLP的解表示为，

  • $x_i, \forall i = 0,…,N-1, x_i \in \{0,1\}$表示设施$i$的开启状况，1表示开启，0表示关闭。
  • $y_{ij}, \forall i = 0,…,N-1, j=0,…,M-1$表示设施$i$满足顾客$j$的需求数。

那么CFLP可以表示为如下的最优化问题，

$$
min \sum_{i=0}^{N-1}\sum_{j=0}^{M-1}c_{ij}y_{ij} + \sum_{i=0}^{N-1}f_ix_i \quad s.t. \\
\begin{align}
y_{ij} \ge 0 & \quad \forall i=0,…,N-1, j=0,…,M-1 \\
\sum_{j=0}^{M-1}y_{ij} \le s_ix_i & \quad \forall i=0,…,N-1 \\
\sum_{i=0}^{N-1}y_{ij} = d_j & \quad \forall j=0,…,M-1 \\
x_i \in \{0,1\} & \quad \forall i=0,…,N-1
\end{align}
$$

CFLP的条件比较多，但您可以将解过程分为两个部分，

  • 开启一些设施（求解$x$）。
  • 决定每个顾客在每个设施中满足需求的数量（将用户需求赋值给设施，求解$y$）。

其中，开启设施共有$2^N$种可能性，也是使得这个问题无法在多项式时间内求解的关键因素。当开启的设施已经被选定时，可以采用如下的贪心策略对设施赋值，

  1. 在已开启且还有容量剩余的设施和还未被满足需求的顾客中选择费用最低的设施-顾客对，尽可能地满足该顾客，直到所有顾客都被满足。
  2. 若该顾客已满足，则将顾客移出考虑范围；若该顾客未被满足，则设施已达到最大容量，将该设施移出考虑范围；特别的，恰好满足时，同时移除设施和顾客；此时如果还有顾客未被满足，则返回1，否则结束过程。

因此，考虑的重点在于选择哪些设施进行开启，下面将着重阐述若干个策略。

实现

Github Repo

  • 实现框架：Golang+Cobra命令行程序

问题的表示

问题包含$N,M,s,f,d,c$五个变量，其中$N,M$用两个整数表示，$s,f$分别用一个长度为$N$的一维数组表示，$d$用一个长度为$M$的一维数组表示，$c$采用一个$N \times M$的二维数组表示，结构如下，

1
2
3
4
5
6
7
8
9
// Problem contains data of a CFLP.
type Problem struct {
    N, M        int
    Capacities  []int
    FixedCosts  []int
    Demands     []int
    TotalDemand int
    Costs       [][]int
}

注：为了计算方便，在读取数据的时候计算了总需求并储存在变量TotalDemand中。

易得，读取数据的时间复杂度为$O(NM)$，空间复杂度为$O(NM)$。

解的表示

一个解包含设施的开启信息$x$和用户需求的赋值信息$y$，分别使用一个长度为$N$的一维数组和一个$N \times M$的二维数组表示，结构如下，

1
2
3
4
5
6
7
// Solution represents a solution of a CFLP.
type Solution struct {
    *Problem
    X       []bool
    Y       [][]int
    RunTime float64
}

注：添加了RunTime记录运行时间。

当X确定时，采用上面提到的贪心策略进行需求赋值的代码过程如下，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
// Assign assigns demands to facility based on current opened facilities.
func (s *Solution) Assign() {
    totalDemand := s.TotalDemand
    filled := make([]int, s.N)
    demands := make([]int, s.M)
    for j := range s.Demands {
        demands[j] = s.Demands[j]
    }
    for i := range s.Y {
        for j := range s.Y[i] {
            s.Y[i][j] = 0
        }
    }
    for totalDemand > 0 {
        // find the cheapest cost
        minI := 0
        minJ := 0
        minCost := math.MaxInt32
        for i := range s.Costs {
            if !s.X[i] || filled[i] == s.Capacities[i] {
                continue
            }
            for j := range s.Costs[i] {
                if s.Costs[i][j] < minCost && demands[j] > 0 {
                    minI = i
                    minJ = j
                    minCost = s.Costs[i][j]
                }
            }
        }

        // assign
        var fill int
        if s.Capacities[minI]-filled[minI] <= demands[minJ] {
            // the facility will be full
            fill = s.Capacities[minI] - filled[minI]
        } else {
            // the facility has more capacity then the demand
            fill = demands[minJ]
        }
        demands[minJ] -= fill
        totalDemand -= fill
        s.Y[minI][minJ] += fill
        filled[minI] += fill
    }
}

可见，该过程须要临时保留每个设施被占用的容量以及每个顾客剩余的需求，因此空间复杂度为$O(N+M)$。

时间上，每次循环内需要便利所有符合条件的设施-用户对的费用，循环内时间复杂度为$O(NM)$，而每次循环过后必定有一个用户得到满足或者某个设施占用容量达到最大，所以循环次数不会超过设施数和用户数的总和，因此整个过程的时间复杂度为$O(NM(N+M))$。

Greedy 贪心策略

在选择设施上进行贪心策略显然不是最优的，但贪心策略的优点在于运行速度快，能够很快地得到一个参考结果，用于对比其他算法的解。

贪心策略非常简单，

  1. 选择设施中未开启的开启费用最少的设施，开启它。
  2. 若开启的设施的总容量小于顾客的总需求，回到1，否则结束。

运行代码片段如下，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
func (s *Solver) solveByGreedy() *Solution {
    // initialize a solution
    sol := s.initSolution()

    // find the cheapest facility and turn it on
    minFPos := 0
    minF := math.MaxInt32
    for i, f := range s.p.FixedCosts {
        if f < minF {
            minFPos = i
            minF = f
        }
    }
    // Open the facility
    sol.Open(minFPos)

    // open from cheaper until all demands can be satisfied
    for !sol.Valid() {
        minFPos = 0
        minF = math.MaxInt32
        for i, f := range s.p.FixedCosts {
            if f < minF && !sol.X[i] {
                minFPos = i
                minF = f
            }
        }
        sol.Open(minFPos)
    }

    // assign the demands
    sol.Assign()

    return sol
}

复杂度分析

整个算法的流程如下，

  1. 初始化解（$O(MN)$）。
  2. 寻找未开启设施中开启费用最低的设施（$O(N)$）。
  3. 若开启的设施无法满足所用顾客的需要，返回2。(最多返回$N$次)
  4. 需求赋值（$O(MN(M+N))$）。

因此，贪心策略的时间复杂度为$O(N^2 + MN(M+N))$。

由于整个过程仅需要保持一个解，空间复杂度为$O(MN)$。

实验结果

在71个问题的问题集上的实验结果如下，

Result Time(s)
p1 12989.953 0.00004
p2 9288.850 0.00007
p3 10488.850 0.00008
p4 11688.850 0.00036
p5 10902.060 0.00008
p6 9832.666 0.00007
p7 11432.666 0.00006
p8 13032.666 0.00016
p9 10980.250 0.00010
p10 10458.043 0.00009
p11 11458.043 0.00006
p12 12458.043 0.00004
p13 11015.048 0.00028
p14 8514.791 0.00006
p15 10114.791 0.00012
p16 11714.791 0.00009
p17 10295.318 0.00006
p18 8543.171 0.00007
p19 10143.171 0.00013
p20 11743.171 0.00009
p21 12235.528 0.00022
p22 11363.414 0.00009
p23 12563.414 0.00005
p24 13763.414 0.00008
p25 78338.667 0.00039
p26 63710.947 0.00032
p27 65310.947 0.00032
p28 66910.947 0.00034
p29 65258.221 0.00040
p30 54927.860 0.00038
p31 56927.860 0.00043
p32 58927.860 0.00145
p33 77701.857 0.00035
p34 53887.154 0.00033
p35 55487.154 0.00035
p36 57087.154 0.00065
p37 101999.196 0.00024
p38 73636.480 0.00020
p39 74636.480 0.00022
p40 75636.480 0.00020
p41 7276.556 0.00021
p42 8068.351 0.00010
p43 6383.929 0.00009
p44 7995.223 0.00021
p45 8089.250 0.00013
p46 6915.251 0.00009
p47 7705.325 0.00015
p48 7874.275 0.00019
p49 6960.522 0.00009
p50 12441.358 0.00025
p51 9382.546 0.00034
p52 13378.456 0.00016
p53 12650.089 0.00019
p54 10536.867 0.00016
p55 12258.408 0.00019
p56 32522.303 0.00113
p57 37322.303 0.00119
p58 48522.303 0.00209
p59 30606.927 0.00110
p60 37243.427 0.00082
p61 40543.427 0.00142
p62 48243.427 0.00082
p63 31843.780 0.00091
p64 34081.806 0.00061
p65 36481.806 0.00061
p66 42081.806 0.00063
p67 32210.447 0.00096
p68 38955.963 0.00073
p69 41955.963 0.00071
p70 48955.963 0.00128
p71 31843.976 0.00096

Brute Force 暴力求解

在$N$比较小时，可以使用暴力求解的方式，即枚举所有设施开启和关闭的可能性（共$2^N$种可能）。暴力求解的时间复杂度为$O(2^N)$，因此当$N$比较大时，这种方法是不适用的，但是暴力求解可以在不清楚最优解的情况下找到一个理论上的最优解，用于比较分析其他求解算法。

暴力求解的代码过程如下，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
func (s *Solver) solveByBruteForce() *Solution {
    // initialize a solution
    var bestSol *Solution
    bestCost := math.MaxFloat64

    // enumerate all situations
    total := 1 << uint(s.p.N)
    for c := 0; c < total; c++ {
        // output intermidiate results
        if c%2000 == 0 {
            log.Printf("evaluating %s(%d/%d) best=%.3f\n",
                strconv.FormatInt(int64(c), 2), c, total, bestCost)
        }
        // initialize a solution
        sol := s.initSolution()
        // open the facilities
        for i := range sol.X {
            if 1<<uint(i)&c > 0 {
                sol.Open(i)
            }
        }
        // if the solution cannot satisfy all customers, skip
        if !sol.Valid() {
            continue
        }
        // assign and compute the cost
        sol.Assign()
        cost := sol.Cost()
        if cost < bestCost {
            bestCost = cost
            bestSol = sol
        }
    }

    return bestSol
}

过程中，通过一个整数$c, 0 \le c < 2^N$来表示$N$个设施的唯一一种开关状态，以其二进制数中的1表示开启，0表示关闭，因此遍历c即可遍历所有情况。

时间复杂度：$O(2^N)$
空间复杂度：$O(MN)$

实际实验过程中，当$N > 20$时运行时间已经不可接受，应当使用其它的一些算法。

实验结果

Result Time(s)
p1 8899.287 0.01975
p2 7943.402 0.01708
p3 9543.402 0.01890
p4 10947.538 0.01488
p5 8928.489 0.00602
p6 7729.489 0.00627
p7 9529.489 0.00606
p8 11259.081 0.00579
p9 8460.030 0.03576
p10 7617.000 0.03523
p11 9103.286 0.03549
p12 10363.911 0.03088
p13 8245.910 63.38475
p14 7125.641 63.63613
p15 8856.372 62.66329
p16 10456.372 61.17692
p17 8195.925 60.36199
p18 7100.582 69.37253
p19 8803.787 66.69740
p20 10403.787 60.53454
p21 8054.758 64.53812
p22 7092.000 64.51618
p23 8740.758 64.48915
p24 10267.971 64.60072
p25 - $\infty$
… - $\infty$
p71 - $\infty$

Simulated Annealing 模拟退火

模拟退火算法是一种优秀的局部搜索算法，它在做邻域搜索的同时，概率接受差解以跳出局部最小值。在CFLP中，将设施的一组开关组合视为一个状态，使用模拟退火算法的基本流程如下，

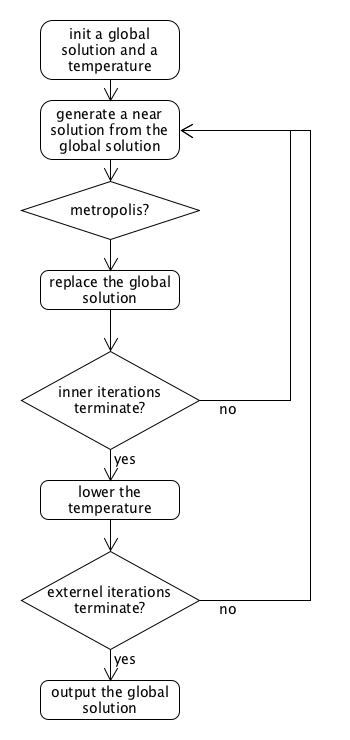
其中，内外层循环终止条件一般设定为经过一定数目的迭代次数后终止。

参数设定

  • 初始温度T=100
  • 内层循环数为1000
  • 外层循环数为1000
  • 温度下降方式为T *= 0.99

初始解的生成

初始全局解应当随机生成，即每个设施按均匀分布决定开或者不开。

邻域搜索

领域搜索即根据当前解生成下一个解，实验过程中发现模拟退火算法里使用多种邻域搜索方式共同作用比单种邻域搜索方式效果要好很多，实验中使用到的备选邻域操作有，

  1. 随机开启/关闭某个设施。
  2. 随机开启/关闭一段连续的设施。
  3. 将某一段连续的设施的开关状态倒置。

当需要生成新状态时，从上述三种方法中随机选择一种。

Metropolis 准则

Metropolis准则是模拟退火算法的核心所在，当这个准则满足时，接受生成的解并替换掉全局解。具体而言，Metropolis准则为

$$
\min\{1, e^{-\frac{C’-C}{T}}\} < R
$$

其中，$C’$为生成的解的费用，$C$为全局解的费用，$T$为温度，$R$为$[0,1]$之间的随机数。

可见，当遇到好解时，$e^{-\frac{C’-C}{T}} > 1$，必定会接收，但当遇到差解时，当温度高时，$e^{-\frac{C’-C}{T}}$比温度低时更加接近1，有概率接收此差解，且随着温度降低，接收差解的概率也降低，最终收敛到一个最优解。

复杂度分析

模拟退火算法的代码过程如下，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func (s *Solver) solveBySA() *Solution {
    // parameters
    bestSol := s.initSolution()
    bestSol.Shuffle()
    for !bestSol.Valid() {
        bestSol.Shuffle()
    }
    bestSol.Assign()
    bestCost := bestSol.Cost()
    nExtIter := 1000
    nInnIter := 1000
    T := 100.0

    // searching
    for ext := 0; ext < nExtIter; ext++ {
        for inn := 0; inn < nInnIter; inn++ {
            sol := CopySolution(bestSol)
            sol.RandomAreaOperate()
            for !sol.Valid() {
                sol.RandomAreaOperate()
            }
            sol.Assign()
            costNext := sol.Cost()
            if math.Min(1, math.Exp(bestCost-costNext)/T) >= rand.Float64() {
                bestSol = sol
                bestCost = costNext
            }
        }
        log.Printf("ExtIter=%d(%d) T=%.3f bestCost=%.3f\n", ext, nExtIter,
            T, bestCost)
        T *= 0.99
    }

    return bestSol
}

其中在内层循环，复制解的复杂度为$O(MN)$，随机邻域操作的平均复杂度为$O(N)$，其余均为常数时间，因此整体算法的时间复杂度为$O(EIMN)$，其中$E$为外层循环数，$I$为内层循环数。

由于整个过程只需保持一个解，空间复杂度为$O(MN)$。

实验结果

在71个问题的问题集上的实验结果如下，

Result Time(s)
p1 8899.287 49.67533
p2 7943.402 46.02201
p3 9549.287 43.71652
p4 10947.538 41.95468
p5 8928.489 49.61210
p6 7729.489 49.43371
p7 9529.489 49.90450
p8 11259.650 49.82498
p9 8460.030 38.91396
p10 7617.000 41.85766
p11 9103.286 39.19025
p12 10363.911 39.63912
p13 8245.910 62.59881
p14 7125.641 63.83618
p15 8856.372 56.31368
p16 10456.372 55.16921
p17 8195.925 62.16191
p18 7129.274 74.85285
p19 8803.787 59.92987
p20 10403.787 59.71305
p21 8139.000 56.84904
p22 7124.000 59.69487
p23 8780.306 54.46691
p24 10298.306 50.47274
p25 12233.713 546.33127
p26 11152.713 540.89889
p27 13117.713 548.15456
p28 15183.478 608.56645
p29 13831.838 3797.52276
p30 12366.202 666.75613
p31 14535.702 642.78949
p32 17277.047 629.18618
p33 12174.419 531.56347
p34 11212.667 585.61782
p35 13843.667 565.90143
p36 14570.419 500.77183
p37 11424.636 427.68900
p38 10594.000 512.98266
p39 11976.636 429.34593
p40 13176.636 428.54124
p41 6755.391 100.04381
p42 5680.069 93.40380
p43 5401.000 80.17776
p44 7162.573 113.07130
p45 6244.500 104.98954
p46 5994.292 95.73207
p47 6424.425 127.02732
p48 5594.600 125.31068
p49 5304.300 98.86595
p50 9258.967 139.52326
p51 7748.878 198.40947
p52 9862.039 167.22943
p53 8969.800 165.41922
p54 9331.120 136.80022
p55 7789.517 157.08357
p56 21422.086 1343.04327
p57 26388.956 1220.42790
p58 37722.381 1176.16916
p59 27645.265 1169.97743
p60 20923.000 1212.31783
p61 25621.657 1052.55700
p62 33197.623 957.01278
p63 25287.956 975.96980
p64 20834.000 1602.66377
p65 25093.000 868.34070
p66 32522.450 762.51041
p67 24932.180 900.71575
p68 20884.000 1051.84617
p69 25202.000 937.94478
p70 32858.727 845.59141
p71 25924.628 923.64509

综合对比

三种算法在71个问题上的实验结果如下，您可以点击此链接下载所有解的详细结果，包括解的最终费用，开启的设施以及顾客的赋值情况。

Result(greedy) Time(s) Result(brute-force) Time(s) Result(sa) Time(s)
p1 12989.953 0.00004 8899.287 0.01975 8899.287 49.67533
p2 9288.850 0.00007 7943.402 0.01708 7943.402 46.02201
p3 10488.850 0.00008 9543.402 0.01890 9549.287 43.71652
p4 11688.850 0.00036 10947.538 0.01488 10947.538 41.95468
p5 10902.060 0.00008 8928.489 0.00602 8928.489 49.61210
p6 9832.666 0.00007 7729.489 0.00627 7729.489 49.43371
p7 11432.666 0.00006 9529.489 0.00606 9529.489 49.90450
p8 13032.666 0.00016 11259.081 0.00579 11259.650 49.82498
p9 10980.250 0.00010 8460.030 0.03576 8460.030 38.91396
p10 10458.043 0.00009 7617.000 0.03523 7617.000 41.85766
p11 11458.043 0.00006 9103.286 0.03549 9103.286 39.19025
p12 12458.043 0.00004 10363.911 0.03088 10363.911 39.63912
p13 11015.048 0.00028 8245.910 63.38475 8245.910 62.59881
p14 8514.791 0.00006 7125.641 63.63613 7125.641 63.83618
p15 10114.791 0.00012 8856.372 62.66329 8856.372 56.31368
p16 11714.791 0.00009 10456.372 61.17692 10456.372 55.16921
p17 10295.318 0.00006 8195.925 60.36199 8195.925 62.16191
p18 8543.171 0.00007 7100.582 69.37253 7129.274 74.85285
p19 10143.171 0.00013 8803.787 66.69740 8803.787 59.92987
p20 11743.171 0.00009 10403.787 60.53454 10403.787 59.71305
p21 12235.528 0.00022 8054.758 64.53812 8139.000 56.84904
p22 11363.414 0.00009 7092.000 64.51618 7124.000 59.69487
p23 12563.414 0.00005 8740.758 64.48915 8780.306 54.46691
p24 13763.414 0.00008 10267.971 64.60072 10298.306 50.47274
p25 78338.667 0.00039 - $\infty$ 12233.713 546.33127
p26 63710.947 0.00032 - $\infty$ 11152.713 540.89889
p27 65310.947 0.00032 - $\infty$ 13117.713 548.15456
p28 66910.947 0.00034 - $\infty$ 15183.478 608.56645
p29 65258.221 0.00040 - $\infty$ 13831.838 3797.52276
p30 54927.860 0.00038 - $\infty$ 12366.202 666.75613
p31 56927.860 0.00043 - $\infty$ 14535.702 642.78949
p32 58927.860 0.00145 - $\infty$ 17277.047 629.18618
p33 77701.857 0.00035 - $\infty$ 12174.419 531.56347
p34 53887.154 0.00033 - $\infty$ 11212.667 585.61782
p35 55487.154 0.00035 - $\infty$ 13843.667 565.90143
p36 57087.154 0.00065 - $\infty$ 14570.419 500.77183
p37 101999.196 0.00024 - $\infty$ 11424.636 427.68900
p38 73636.480 0.00020 - $\infty$ 10594.000 512.98266
p39 74636.480 0.00022 - $\infty$ 11976.636 429.34593
p40 75636.480 0.00020 - $\infty$ 13176.636 428.54124
p41 7276.556 0.00021 - $\infty$ 6755.391 100.04381
p42 8068.351 0.00010 - $\infty$ 5680.069 93.40380
p43 6383.929 0.00009 - $\infty$ 5401.000 80.17776
p44 7995.223 0.00021 - $\infty$ 7162.573 113.07130
p45 8089.250 0.00013 - $\infty$ 6244.500 104.98954
p46 6915.251 0.00009 - $\infty$ 5994.292 95.73207
p47 7705.325 0.00015 - $\infty$ 6424.425 127.02732
p48 7874.275 0.00019 - $\infty$ 5594.600 125.31068
p49 6960.522 0.00009 - $\infty$ 5304.300 98.86595
p50 12441.358 0.00025 - $\infty$ 9258.967 139.52326
p51 9382.546 0.00034 - $\infty$ 7748.878 198.40947
p52 13378.456 0.00016 - $\infty$ 9862.039 167.22943
p53 12650.089 0.00019 - $\infty$ 8969.800 165.41922
p54 10536.867 0.00016 - $\infty$ 9331.120 136.80022
p55 12258.408 0.00019 - $\infty$ 7789.517 157.08357
p56 32522.303 0.00113 - $\infty$ 21422.086 1343.04327
p57 37322.303 0.00119 - $\infty$ 26388.956 1220.42790
p58 48522.303 0.00209 - $\infty$ 37722.381 1176.16916
p59 30606.927 0.00110 - $\infty$ 27645.265 1169.97743
p60 37243.427 0.00082 - $\infty$ 20923.000 1212.31783
p61 40543.427 0.00142 - $\infty$ 25621.657 1052.55700
p62 48243.427 0.00082 - $\infty$ 33197.623 957.01278
p63 31843.780 0.00091 - $\infty$ 25287.956 975.96980
p64 34081.806 0.00061 - $\infty$ 20834.000 1602.66377
p65 36481.806 0.00061 - $\infty$ 25093.000 868.34070
p66 42081.806 0.00063 - $\infty$ 32522.450 762.51041
p67 32210.447 0.00096 - $\infty$ 24932.180 900.71575
p68 38955.963 0.00073 - $\infty$ 20884.000 1051.84617
p69 41955.963 0.00071 - $\infty$ 25202.000 937.94478
p70 48955.963 0.00128 - $\infty$ 32858.727 845.59141
p71 31843.976 0.00096 - $\infty$ 25924.628 923.64509

可以发现，模拟退火的算法要远好于贪心算法，并且与有结果的暴力求解的结果十分相近。