Summary
493 is a typical question using the divide-and-conquer method. In fact, we can add only a little process into the general merging procedure of the mergesort to accomplish this task.
Solution by Mergesort
In the general mergesort process, we merge two sorted list into one by moving two indexes in each list. For example, consider two sorted list L=[1, 3, 5, 7] and R=[2, 4, 6, 8]. Let i, j be the indexes. The initial state is
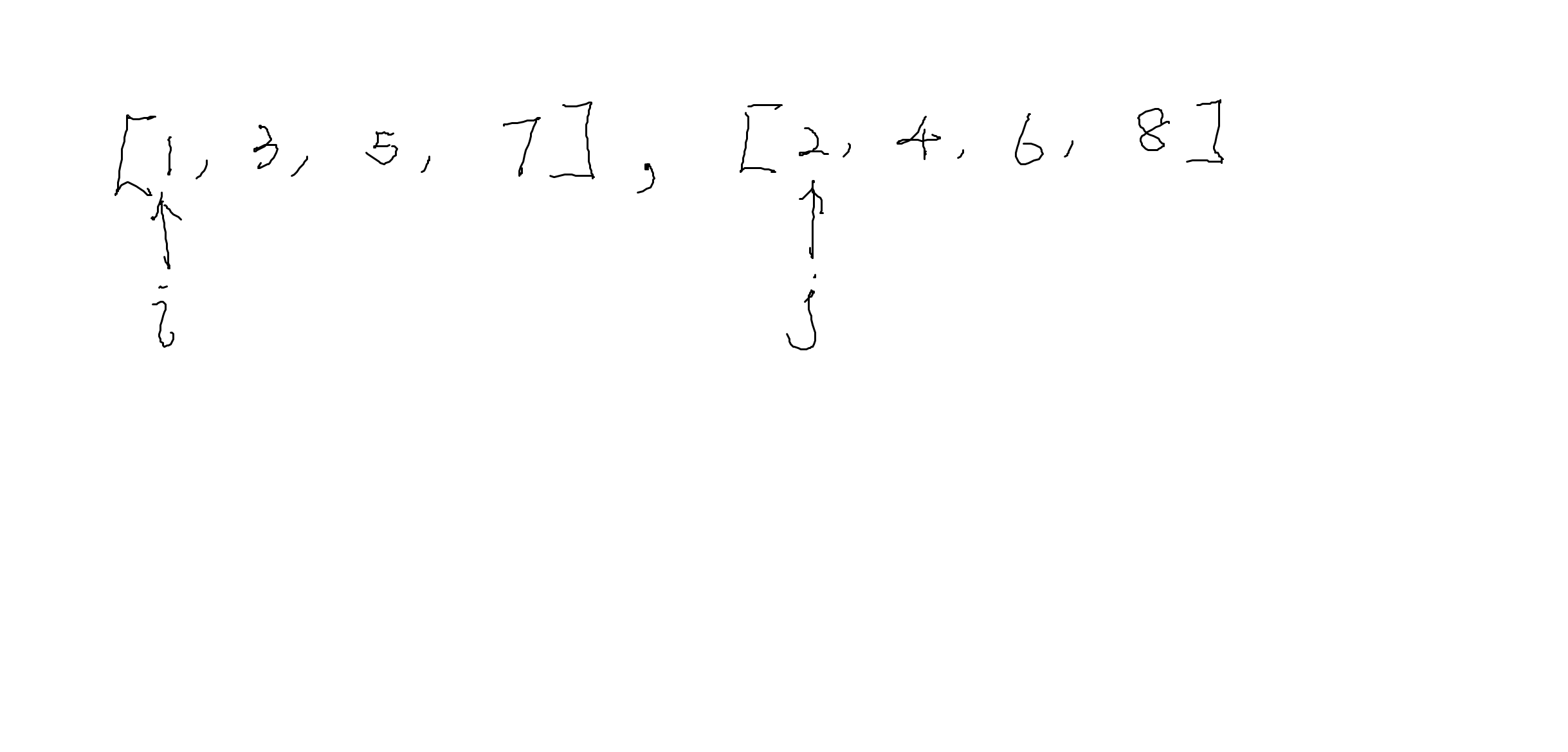
We compare the R[i] and L[j] and put the smaller one to the new list. After that, the smaller one's index move to next one.
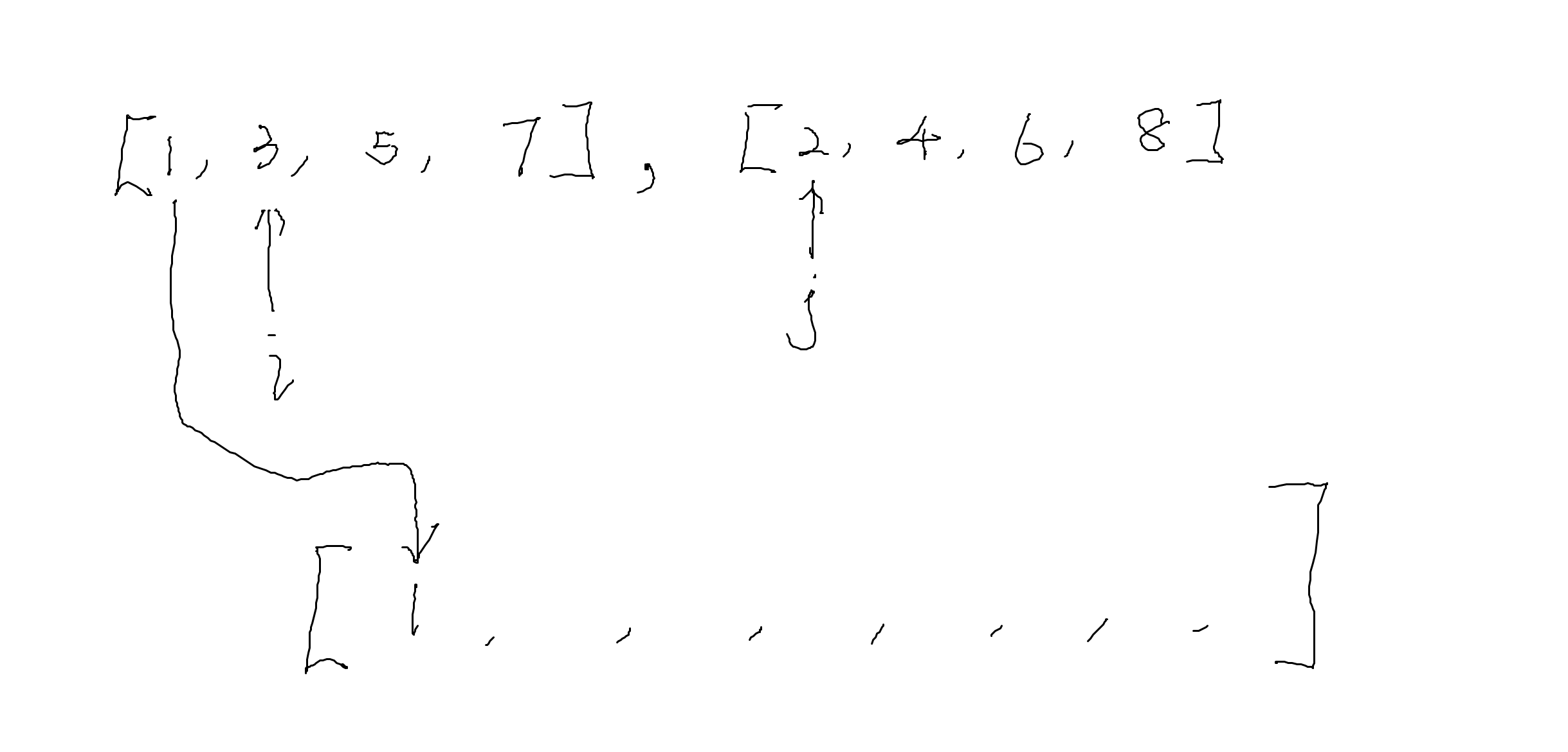
This process continues until the big list is filled up.
In 493, what we need to do is just repeat this process similarly once before this process. We still use two indexes and compare the values, but at this time, we should compare L[i] and 2 * R[j].
If L[i] > 2 * R[j], then we can make sure that all the elements after i in L are also bigger than 2 * R[j] because L is sorted. Thus, we just need to add L.size() - i to the total number and move j to the next one.
If L[i] <= 2 * R[j], just move i to the next one.
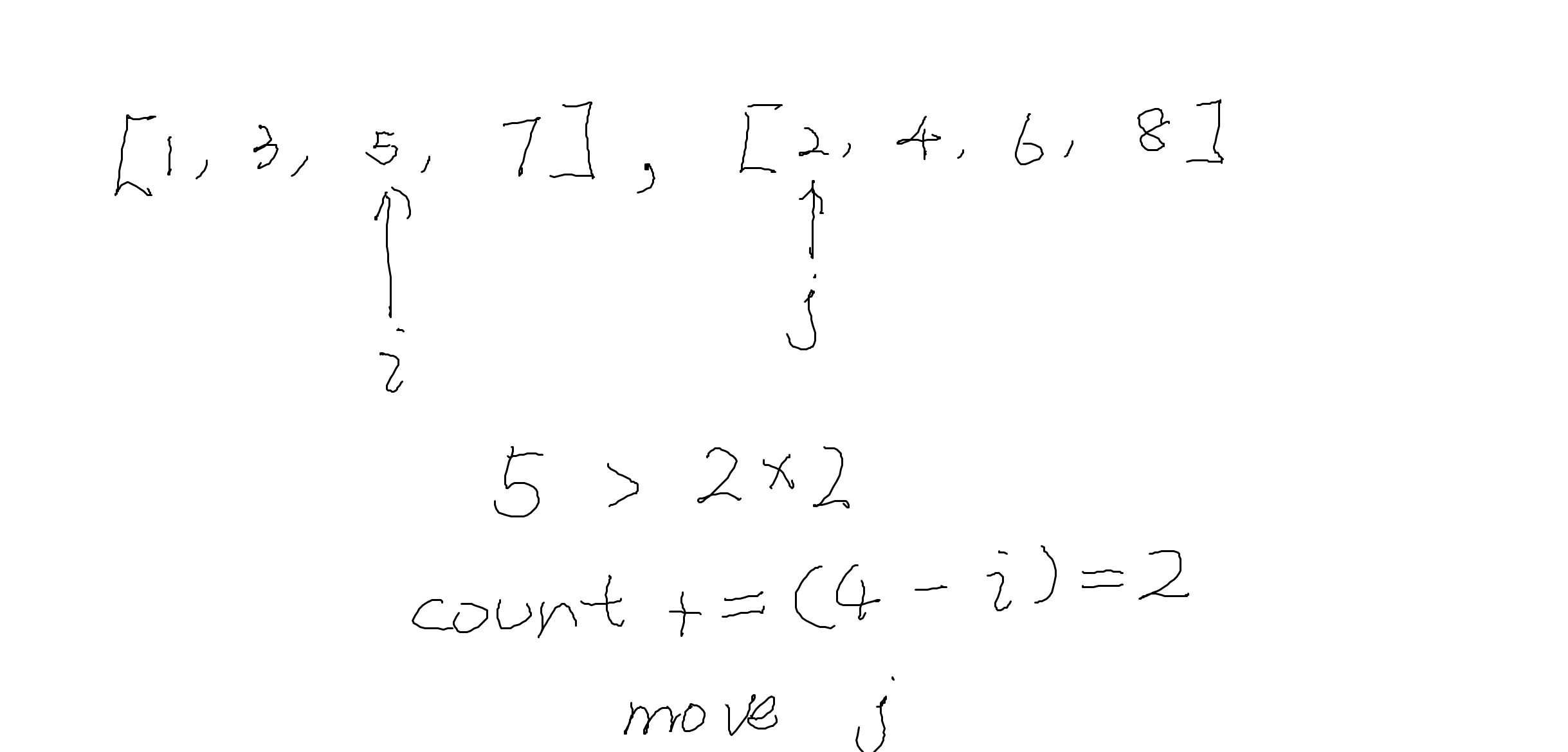
Finally, what we get is two processes. The first one is comparing L[i] and 2 * R[j] and modify the number of reverse pairs, and the second one is the general merging process of the mergesort. The two processes only access each element once, so the time complexity is $O(n)$. With the division process time complexity $O(logn)$, the total time complexity of this solution is $O(nlogn)$.