The principles and techniques for compiler design are applicable to so many other domains that they are likely to be reused many times in the career of a computer scientist. The study of compiler writing touches upon programming languages, machine architecture, language theory, algorithms, and software engineering.

The General Structure of a Compiler

Context-Free Grammars

A context-free grammar $G$ is defined by the 4-tuple

$$
G = (V, \Sigma, R, S)
$$

where

$V$ is a set of nonterminals, sometimes called "syntactic variables." Each nonterminal represents a set of strings of terminals, in a manner we shall describe.
$\Sigma$ is a set of terminal symbols, sometimes referred to as "tokens." The terminals are the elementary symbols of the language defined by the grammar.
$R$ is a set of productions, where each production consists of a nonterminal, called the head or left side of the production, an arrow, and a sequence of terminals and/or nonterminals, called the body or right side of the production. In fact, $R$ is a finite relation from $V$ to $(V \cup \Sigma)^*$.
$S$ is designation of one of the nonterminals as the start symbol.

All the terminal strings that can be derived from the start symbol form the language defined by the grammar.

Important Concepts in Lexical Analysis

A token is a pair consisting of a token name and an optional attribute value. The token name is an abstract symbol representing a kind of lexical unit, e.g., a particular keyword, or a sequence of input characters denoting an identifier. The token names are the input symbols that the parser processes. In what follows, we shall generally write the name of a token in boldface. We will often refer to a token by its token name.

A pattern is a description of the form that the lexemes of a token may take. In the case of a keyword as a token, the pattern is just the sequence of characters that form the keyword. For identifiers and some other tokens, the pattern is a more complex structure that is matched by many strings.

A lexeme is a sequence of characters in the source program that matches the pattern for a token and is identified by the lexical analyzer as an instance of that token.

An alphabet is any finite set of symbols.

A string over an alphabet is a finite sequence of symbols drawn from that alphabet.

A language is any countable set of strings over some fixed alphabet.

A regular set is a language that can be defined by a regular expression.

Regular Expressions

Regular expressions are defined by the following rules:

$\epsilon$ is a regular expression, and $L(\epsilon)=\{\epsilon\}$.
If $a \in \Sigma$, then $a$ is a regular expression, and $L(a) = \{a\}$.

Suppose $r$ and $s$ are regular expressions.

$r|s$ is a regular expression and $L(r|s)=L(r) \cup L(s)$.
$rs$ is a regular expression and $L(rs)=L(r)L(s)$.
$r^*$ is a regular expression and $L(r^*)=L(r)^*$.
$(r)$ is a regular expression and $L((r))=L(r)$.

There are also plenty of extensions of regular expressions.

$r^+$ is a regular expression and $L(r^+)=L(r)^+$.
$r?$ is a regular expression and $L(r?)=L(r) \cup \{\epsilon\}$.
$[a_1a_2\cdots a_n]$ is a regular expression with $a_1,a_2,\cdots,a_n$ are all regular expressions and it is a shorthand of $a_1|a_2|\cdots|a_n$.

Regular expressions have following properties:

$r|s=s|r$.
$r|(s|t)=(r|s)|t$.
$r(st)$=$(rs)t$.
$r(s|t)=rs|rt$; $(s|t)r=sr|tr$.
$\epsilon r=r\epsilon=r$.
$r^*=(r|\epsilon)^*$.
$r^{**}=r^*$.

Finite Automata

Finite automata are recognizers: they simply say "yes" or "no" about each possible input string.

Nondeterministic Finite Automata

A nondeterministic finite automaton(NFA) is defined by a 5-tuple, $(S, \Sigma, T, s_0, F)$, consisting of

A finite set of states $S$.
A set of input symbols $\Sigma$, the input alphabet. We assume that $\epsilon$ is never a member of $\Sigma$.
A transition function $T$ that gives, for each state, and for each symbol in $\Sigma \cup \{\epsilon\}$ a set of next states.
A state $s_0$ from $S$ that is distinguished as the start state or the initial state.
A set of states $F$, a subset of $S$, that is distinguished as the accepting states or the final states.

Deterministic Finite Automata

A deterministic finite automaton(DFA) is a special case of an NFA where:

There are no moves on input $\epsilon$.
For each state $s$ and input symbol $a$, there is exactly one edge out of $s$ labeled $a$.

Algorithm: From NFA to DFA

INPUT An NFA $N$.

OUTPUT A DFA $D$ accepting the same language as $N$.

STEPS

Compute $\epsilon\text{-}closure(s_0)$ as the initial unmarked state $s_0’$ of $D$.
Do the following until all the states in $D$ is marked:
1. Pick up an unmarked state $s’$ in $D$, mark $s’$.
2. For all symbols $a$ in $\Sigma$, do the following:
  1. Compute $\epsilon\text{-}closure(move(S_{s’}, a))$ as a state $s_i’$ in $D$, where $S_{s’}$ is the set of states in $N$ corresponding to the the state $s’$ in $D$.
  2. If $s_i’$ is not a existed state of $D$, add it as an unmarked new state.
  3. Create an edge $a$ between $s’$ and $s_i’$.

EXPLANATION

$\epsilon\text{-}closure(s)=\{s | s\text{ can be reached from }s_0\text{ through an edge labeled }\epsilon\}$.
$move(S,a)=\{s|s\text{ can be reached from states in }S\text{ through an edge labeled }a\}$.

Algorithm: Simulating an NFA

INPUT An input string $x$ terminated by an end-of-file character eof. An NFA $N$.

OUTPUT Answer "true" if $N$ accepts $x$; "false" otherwise.

STEPS

Compute $S=\epsilon\text{-}closure(s_0)$, where $s_0$ is the start state of $N$.
Do the following until an eof is read:
1. Read a character $c$.
2. Let $S=\epsilon\text{-}closure(move(S,c))$.
If $S \cap F \ne \emptyset$, answer "true" and otherwise, answer "false".

Algorithm: Constructing an NFA from a Regular Expression

INPUT A regular expression $r$ over alphabet $\Sigma$.

OUTPUT An NFA $N$ accepting $L(r)$.

METHOD

Apply the following rules.

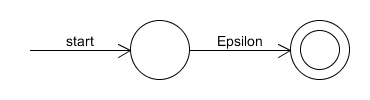
The NFA accepting $L(\epsilon)$ is

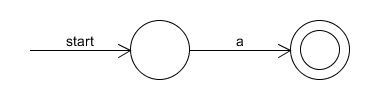
The NFA accepting $L(a)$, where $L(a)=\{a\}$, is

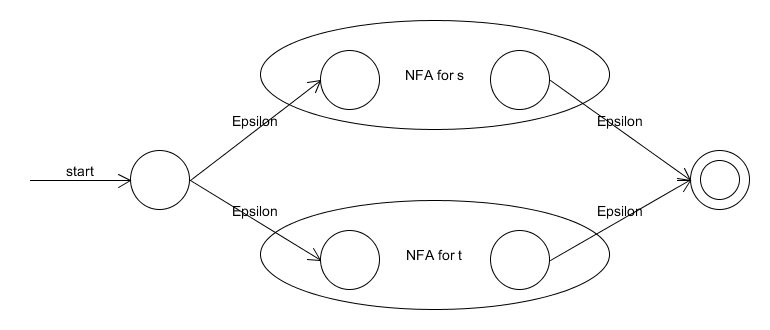
The NFA accepting $L(s|t)$, where both $s$ and $t$ are regular expressions, is

The NFA accepting $L(st)$, where both $s$ and $t$ are regular expressions, is

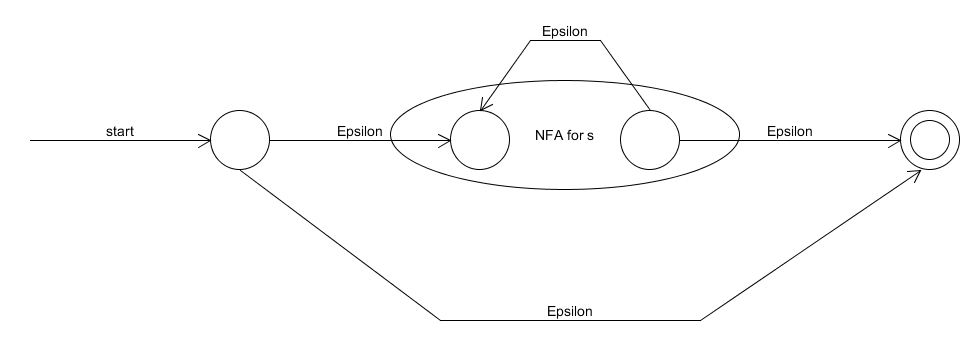
The NFA accepting $L(s^*)$, where $s$ is a regular expression, is

Algorithm: Constructing a DFA from a Regular Expression

INPUT A regular expression $r$ over alphabet $\Sigma$.

OUTPUT A DFA $D$ accepting $L(r)$.

STEPS

Construct a syntax tree $T$ from the augmented regular expression $(r)\#$, and give each leaf a number, called a position. Note that all the leaves of $T$ is a single symbol.
Compute $firstpos(n_0)$ as the unmarked start state $s_0$ of $D$, where $n_0$ is the root of $T$.
Do the following until all the states in $D$ is marked:
1. Pick up an unmarked state $s$ in $D$, mark $s$.
2. For all symbols $a$ in $\Sigma$, do the following:
  1. Compute $followpos(p)$ for all $p$ in $s$ whose symbol in $T$ is $a$ as a state $s_i$.
  2. If $s_i$ is not a existed state of $D$, add it as an unmarked new state.
  3. Create an edge $a$ between $s$ and $s_i$.

EXPLANATION

$firstpos(n)=\{\text{some positions in the subtree rooted at node }n\}$
Suppose the language expressed by the subtree rooted at $n$ is $L(T_n)$, and all the possible first symbols of strings in $L(T_n)$ form a set $\sigma$. $firstpos(n)$ is the set of positions corresponding to the symbols in $\sigma$.
$followpos(p)=\{\text{positions corresponding to all the symbols that are possibly the next one of position }p\}$

Algorithm: Minimizing the Number of States of a DFA

INPUT A DFA $D=(S, \Sigma, T, s_0, F)$.

OUTPUT A DFA $D’$ accepting the same language as $D$ and having as few states as possible.

STEPS

Let $\Pi = {F, S-F}$ be the initial partition.
Do the following until $\Pi$ remains the same:
For each group $G$ in $\Pi$, partition $G$ into subgroups such that two states $s$ and $t$ are in the same group if and only if for all input symbols $a$, state $s$ and $t$ have transitions on $a$ to states in the same group of $\Pi$.
Choose one state of each group in $\Pi$ as the representative for that group, which is also a state in $D’$. The start/accepting state of $D’$ is the representative of the group containing the start/accepting state of $D$.

References

Alfred V. A., et al. Compilers Principles, Techniques, & Tools Second Edition

Context-Free Grammar - Wikipedia. https://en.wikipedia.org/wiki/Context-free_grammar