Problem Link

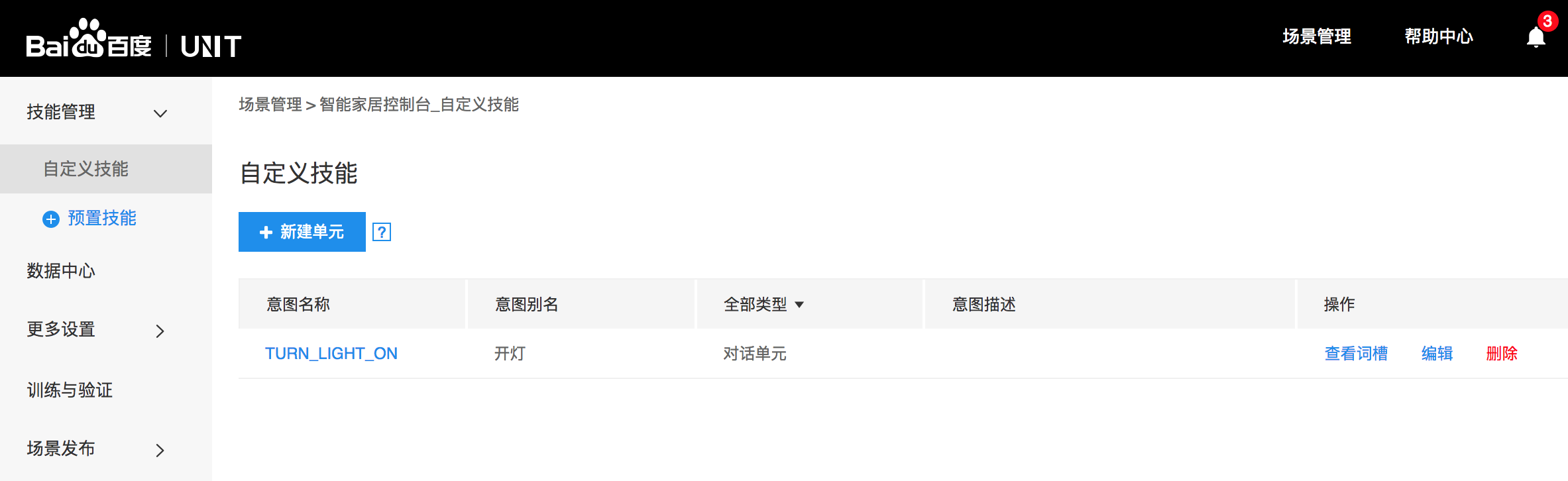
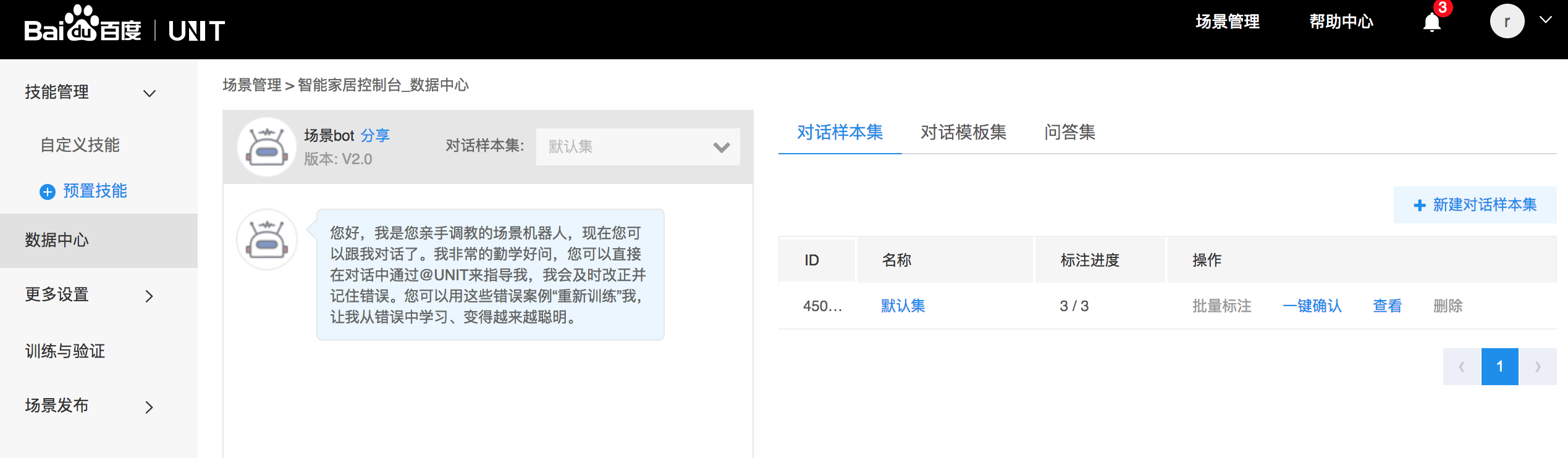
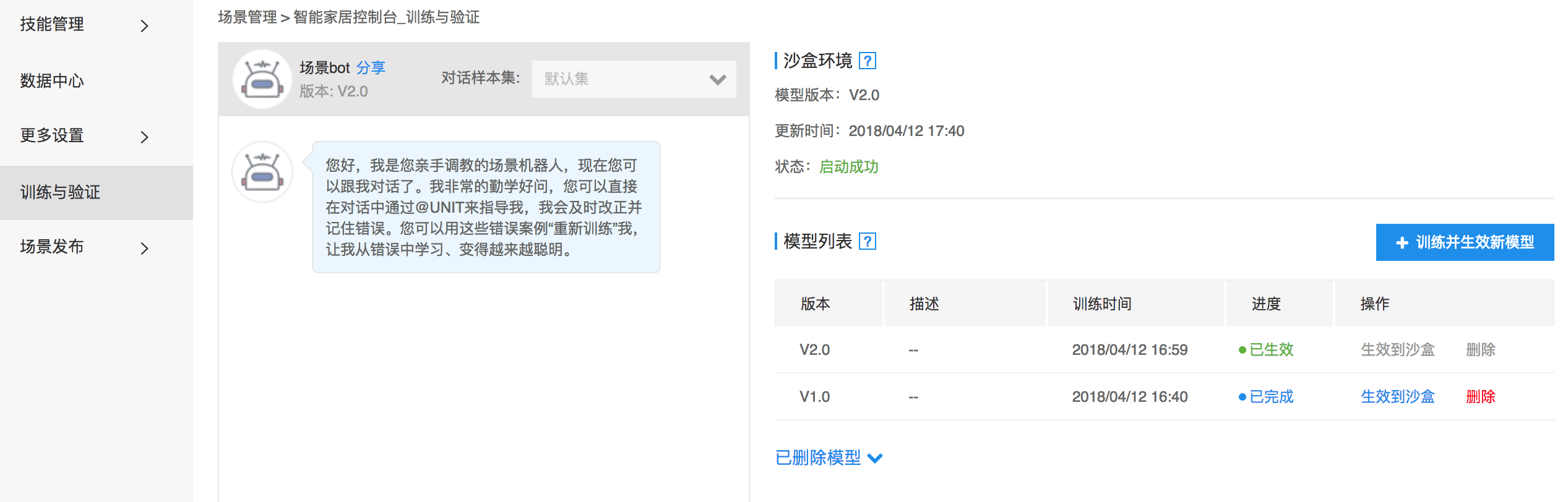
Summary

Given a non-empty string s containing digits from 0 to 26 with size n, determine the total number of ways to decode it by characters ‘A’ to ‘Z’.

Dynamic Programming

This is a typical dynamic programming problem on a sequence. It is not quite hard to come out the representation of states but, in this problem, several situations need to be considered.

At the beginning, I used F[i] to represent the answer of the subsequence from 0 to i, both inclusively. However, it was quite hard to determine the relationships between F[i] and F[i - 1]. Therefore, I came out another representation.

• Let F[i] be the answer of the subsequence from 0 to i, both inclusively, whose all decode ways are end by the character at position i.
• Let G[i] be the answer of the subsequence from 0 to i, both inclusively, whose all decode ways are end by the character combined by position i and i - 1.
• The final answer will be F[n - 1] + G[n - 1].

After that, we need to consider following rules,

1. F[0] = 1, G[0] = 0.
2. s[i] can be along(s[i] != '0'), so F[i] = F[i - 1] + G[i - 1].
3. s[i] cannot be along, so F[i] = 0.
4. s[i] can combine with s[i - 1], so G[i] = F[i - 1].
5. s[i] cannot combine with s[i - 1], so G[i] = 0.
6. There is a 0 in the string, and no other digits can combine with it.
7. s[0] == '0', and the answer is 0.

Therefore, for any 1 <= i < n, we may consider two boolean value, can_along and can_combine. If both of them are false, Rule 6 satisfies and just return 0.

Appendix

Problem Link

概要

硬核DP问题，本问题设计状态转移方程较为困难。

给定初始位置pos为0，速度speed为1的“汽车”，有两种指令A(Accelerate)和R(Reverse)可供使用：

• A指令可使汽车的位置变为pos + speed，同时speed *= 2；
• R指令可重置汽车的速度为1，且方向相反。（您可能会担忧速度为0的情况，但这种情况并不存在）

现给出一个目标位置target，求出到达此位置使用的最少的操作数目。

动态规划

状态定义如下：

令F[i]表示到达位置i所需要的最少操作数目。

状态转移方程的定义涉及到几种情况的讨论，首先定义好边界条件：

F[0] = 0

其次，设计状态转移方程时要考虑到3种情况，为了说明清楚这些情况，您需要在脑中描绘一根数轴。初始时，汽车处于原点位置，考虑汽车永远不进行R操作，一直往前开的情况，很容易发现，进行n次A操作到达的位置为$2^n - 1$，假定目的地为t，那么有

1. 存在$n \in N$，使得$t = 2^n - 1$，那么此时的答案F[t] = n。一路往前开即使最优解，任何的倒车操作都是无用的。

2. 汽车开过了位置t，并从t右侧开回到t。

   这种情况下，要明白一个重要事实：

   汽车一定会在刚刚开过t时执行R操作反向，没有必要继续远离t往前开。

   由于从位置$2^n - 1$能够反向回到$2^{n - 1}$且所需的步数与从$0$到$2^{n - 1} - 1$所需步数一致（可以参考这个例子，0->1->3->7->15->15->14->12->8，从15到8经过3步，从0到7也经过3步），因此若继续往前开，反向后经过一定的步数后必定会回到上个位置，因此往前开是徒增花费的无意义动作。

   因此，这种情况下，可以得到下列状态转移方程：

   F[i] = n + 1 + F[n - i]

   其中，n = ceil(log2(i))，代表距离t最近的右侧的能够全程加速开到的位置，开到后，执行反向操作R耗费1点，之后以位置n为原点，看作是一个从0到位置n - i的子问题。

3. 汽车未开过位置t，进行了反向操作。

   在这种情况下，汽车会在到达位置t之前至少进行两次R操作，调整其位置。那么在这种情况下，可以得到下列状态转移方程：

   F[i] = j + k + 2 + F[i - (2^j - 2^k)]

   其中，j表示第一段连续的A操作的个数，k表示第一次反向后倒退的A操作的个数，2表示两次反向操作，而后可以看作是从新位置到位置i的一个子问题，其中新位置等于前进距离与倒退距离的差$(2^j - 1) - (2^k - 1)$。这里要注意j和k的取值范围，j的范围是0 <= j < n，因为当前情况下不得开过位置t；k的取值范围是0 <= k < j，当k == 0时代表原地重置速度，当k == j时则相当于没开。

综上所述，可以得到状态及状态转移方程如下：

F[i]表示到达位置i所需要的最少操作数目

1
2
3
4
5
6
7

F[0] = 0
n = ceil(log2(i + 1))
if (i == 2^n - 1) {
    F[i] = log2(i + 1)
} else {
    F[i] = min{n + 1 + F[n - i], min(0<=j<n, 0<=k<j){j + k + 2 + F[i - (2^j - 2^k)]}} \\ 情况2和3中取最小，3须枚举一下j, k的值。
}

未证明 情况3中j可固定为n - 1。

附录

Problem Link

概要

在一个数组中选出和最大的互不相邻的子序列，输出其和。

动态规划

作为入门级的动态规划问题，本题实现是非常简单的。本问题与0/1背包问题十分相似，最重要的是想明白动态规划的基本原理。

本题须按照动态规划的思路划分子问题。分治、贪心和动态规划各有不同的角度看待一个问题的子问题，就本题来说，从动态规划的角度出发，对于某一个位置为i的数，只有“选择”和“不选择”两种选择，我们须取这两种选择中和比较大的那个，那么定义长度为i的数组arr的所求最大和为F[i]，则有

F[i] = max(arr[i] + F[i - 2], F[i - 1])

其中，max函数的第一个参数表示选择位置为i的数所得结果，第二个参数表示不选择，通过这样的方式将原问题划分为了两个子问题。

显然，并不需要递归来实现这个式子，最终仅需要一次遍历，在常数的空间复杂度内即可求得结果F[n]。

附录

prevMax代表F[i - 1]， pprevMax代表F[i - 2]，这两个值并不需要全部保留，每轮进行更新即可。

Problem Link

总览

N对情侣希望坐在2N个座位上，每个情侣希望坐到相邻的位置，请通过最少次的座位交换达成此目的。

贪心算法

本题目看似可以进行状态搜索，但实际上状态空间十分巨大，很难做到。直观来看，每一次交换至少可以使一对情侣坐到一起，且至多可使两对情侣坐到一起。

很容易想到如下贪心策略：

• 每次令最左边的一对情侣坐到一起，将其移出，重复此操作直至所有情侣都坐到一起。

事实上这个策略是正确的，您可能会有一些顾虑，例如

1. 当次交换可能可使两对情侣坐到一起，但却没有执行这个操作。
2. 可能存在更好的交换选择，使得后面尽可能多地出现“能恰好使两对情侣坐到一起”的情况。

对于1，可以想到的是即使当次没有那两对情侣，但这并不影响后面进行这步操作，因为当次交换一定不会涉及到互相坐错的两对情侣的位置。

对于2，实际上这种情况并不存在。一次交换至多产生两个“相互坐错”的情况，但仅当当次交换是一次无用的交换（没有使任何情侣坐到一起），才有可能产生两个“相互坐错”，这种情况下算上这次无用的交换依然要交换三次，因此有用的交换至少不会比无用的交换差；其次如果某个交换能够产生一个“相互坐错”，其他情侣的配对并不会影响到这个交换之后的实施，因此这样做是没有问题的。

附录

Problem Link

概要

给定一个非负整数的数组，从起始位置开始跳跃，每个数字代表能够跳跃的最大距离，判断是否能够跳跃到末尾位置。

贪心算法

回顾贪心算法的两个要素：

• 在当前状态能够找到一个安全的行动；
• 问题具有最优子结构。

很容易看出，本题具有最优子结构。每次将跳跃到的位置之前的元素删除，即可得到与原问题性质一致、但规模较小的子问题——在剩下的较小的数组中判断是否能从起始位置跳到末尾位置。因此尝试使用贪心算法解决本问题。

现在应当考虑如何进行安全的一步操作，以制定贪心策略，进一步来说，问题可以理解成视解为下标的一个序列，能否跳跃到一个在这个序列当中的一个位置。

错误的贪心策略可能有：

• 从起始位置出发，每次跳跃到最远的位置。
• 从起始位置出发，每次跳跃到数字最大的位置。
• 从起始位置出发，每次跳跃到能够到达的位置的值之和最大的位置。
• …

要注意的是，数组的起始位置不一定在解当中，因此从起始位置起步是不合适的，从末尾位置开始才是正解。

正确的贪心策略是：

从末尾位置出发向前找，每次找一个能够跳到末尾位置的位置，并从这个新位置出发重复寻找操作，直到回到了起始位置（成功）或无法再往前跳跃（失败）。

这样确保了每次都能找到一个在解中的位置，并且当多个位置满足要求时，由于它们都能到达同一个位置，这些位置也是相互能回溯到的。

如此这般，本题能够在遍历一遍数组（$O(n)$)的情况下返回结果。

附录

Problem Link

概要

定义两个字符串X和Y相似如下：

交换X中任意两个字符的位置一次，得到字符串Y。

给定一个所有字符串长度相同的字符串数组，求出其中两两相似的字符串的集合数。

题解

将字符串看作“顶点”，将相似看作“边”，那么本题要求解的就是这个无向图中连通分量的个数；而对于一个无向图，仅需要一次深度优先搜索即可得到连通分量的个数。因此，本题可以分解为以下几个基本步骤：

• 求图
• 深度优先搜索

求图

对于数组中的字符串进行遍历，判断两两是否相似，相似则构建一条无向边。判断相似则是遍历数组X，找到前两个与Y不相同的字符，交换其位置并判断是否相等。设数组长度为$n$，字符串长度为$m$，那么这一步的时间复杂度为：

$$
O(n^2m)
$$

深度优先搜索

得到这一张无向图之后，对其进行深度优先搜索即可得到连通分量的个数，这一步的复杂度为点数与边数的和，顶点数已确定为$n$，那么在最坏情况下，一张全连通图的边数为

$$
\frac{n(n-1)}{2}
$$

那么这一步的时间复杂度为

$$
O(n^2)
$$

因此整个算法的时间复杂度为

$$
O(n^2m)
$$

本题除了要用到图论的思想外，自顶向下逐步分解也是比较重要的。

附录

Problem Link

概要

本题要在一个数组中寻找子数组，使得其和落在指定区间内，输出满足条件的数组的个数。要求复杂度低于$O(n^2)$。

方法一 暴力求解

您很容易想到$O(n^2)$的暴力求解方法，仅须两层循环将所有子序列的和求出来即可，代码简单，运行的结果也很明了——TLE。

方法二 修改版归并排序

事实上，本题是一个归并排序的题目。

Step 1 求前n项和数组

由于寻找子数组是一个十分麻烦的事情，首先要将原问题进行转化。很容易想到，对于序列$a_i$，任意一个子序列的和

$$
S(a)_{ij} = S(a)_i - S(a)_j
$$

因此对于输入长度为$n$的数组$A$，可以求得一个长度为$n+1$的前n项和数组$S$，那么问题就转化为在该数组中寻找一个元组$(i, j)$，使得

$$
lower \le S_j - S_i \le upper, i \le j
$$

因此算法的第一步是求前n项和数组$S$，遍历一遍数组即可，复杂度为$O(n)$。

Step 2 分治

最容易想到的分治就是对半分，本题用对半分对原问题进行分解也是足够的。求给定前n项和数组满足条件的元组个数，先求其前半部分的元组个数，再求其后半部分的元组个数，最后进行组合。根据大师定理，有复杂度的递归表达式

$$
T(n) = 2T(\frac{n}{2}) + O(?)
$$

要使得复杂度低于$O(n^2)$，表达式最后的项也必须低于$O(n^2)$，也就是组合的过程复杂度不能出现两层循环。

直观来看，对于两个长度为$\frac{n}{2}$的子数组，已知各自满足条件的元组个数，那么剩下的事情就是各自寻找一个元素组成元组，看是否满足题目要求——后面的与前面的差落在给定范围内，显然，对于两个无序的数组是很难做到复杂度低于$O(n^2)$的，那么考虑将数组排序。

对于两个有序的数列，可以在$O(n)$的复杂度内找到满足条件的元组个数，令两个数组为$L$，$R$，首先有，如果

$$
R_m - L_i \ge lower \
R_n - L_i \le upper \
m \le n
$$

那么与$L_i$能组成的元组个数即为$n - m$，其次有一个简单但是十分的重要发现，若有

$$
R_m - L_i < lower \
R_n - L_i \le upper
$$

则，

$$
R_m - L_k < lower \ \forall k \in [0, i] \
R_n - L_k \le upper \ \forall k \in [0, i]
$$

也就是说，对于每一个在$L$中的元素，并不需要便利所有$R$中的元素以找到$m, n$的值，由于$m, n$的值只会增加，不会减少，因此对于所有$L$中的元素仅须便利一次$R$即可，复杂度降为$O(n)$。

那么最后的问题就是如何得到两个有序的子数列，直接排序会使得复杂度提升为$O(nlogn)$，显然是行不通的。很容易看到这个分治的过程与归并排序的过程一致，因此在过程中“顺便”给每个子数组进行归并排序即可，即把当前的计数求出来后，将两个数组按归并排序算法合成即可，复杂度为$O(n)$。

最终，根据大师定理，对于递归表达式

$$
T(n) = 2T(\frac{n}{2}) + O(n)
$$

整个算法的复杂度为$T(n) = O(nlogn)$，题目也接受了这个复杂度，Accepted。

附录

用了一个std::inplace_merge简化了归并操作，注意要先向下分解，从最底层开始求次数、归并。

传送门

总览

本题目要求以对数级别的时间复杂度求得两个“有序”数组“共同”的中位数。虽然在时间复杂度上看似有十分严格的要求，但在掌握了题目的核心要点之后，您会发现本题实际上并不困难。

方法一 数组合并

直接将两个数组合并成一个数组，并取其中位数是最直观能想到的办法，但是显而易见的是这个方法的时间复杂度肯定是多项式级别。若两个数组的长度分别是$m$、$n$，那么将这两个数组合并须遍历一遍合并之后得到的数组，即时间复杂度为

$$
O(m+n)
$$

显然，这并不是满足题目要求的算法。（然而我做的时候这个算法居然通过了，速度还和二分查找方法一致）

方法二 二分查找

如果您想到一些目标是$O(logn)$的优化方法，例如二分法、二叉树等，但是并不知道该如何应用到本题上的话，可能是您对中位数的理解还不够透彻。在本题中，要从两个数组中找到中位数，可以考虑如下思路，

• 将数组重新组合成长度相等或长度相差不超过1；
• 两个数组必须满足某一个的最大值不大于另一个的最小值。

对于两个长度分别为$m$和$n$的有序数组$X$、$Y$，一定存在下标$i$，$j$，使得$X[0:i]$与$Y[0:j]$组成的数组$L$和$X[i:m]$与$Y[i:n]$组成的数组$R$满足上述两个条件，并且$i$与$j$满足如下关系，

$$
i + j = m - i + n - j
$$

即

$$
j = \frac{m + n - 2i}{2}
$$

同时，考察$Left$的最后一个值和$Right$的第一个值，即可得到中位数。换言之，只要求得$i$，本题得解。

问题已经转化为求分割数组$X$的那个下标，这时很自然的就可以想到使用复杂度为$O(logn)$二分查找，对于有序数组$X$，设正确分割的下标为$i_0$，对于下标$i$，得到$L$，$R$，则有

$$
L[i] > R[0] \wedge L[i] = X[i] \Rightarrow i > i_0 \
L[i] > R[0] \wedge L[i] = Y[j] \Rightarrow i < i_0 \
L[i] <= R[0] \Rightarrow i = i_0
$$

通过上述条件，可以判断真实值是在当前值的前边还是后边，满足二分查找的条件，可用二分查找得到$i_0$。

特别的，原数组为空时要做特殊处理。

这个方法的时间复杂度与二分查找的时间复杂度相同，本质上说，本题是一个二分查找的题目。

附录

（倒是花了很多时间在边界和特殊情况处理上）

A domain model is a system of abstractions that describes selected aspects of a sphere of knowledge, influence or activity (a domain). The model can then be used to solve problems related to that domain. The domain model is a representation of meaningful real-world concepts pertinent to the domain that need to be modelled in software. The concepts include the data involved in the business and rules the business uses in relation to that data.

领域模型是您在使用UML解决软件需求问题时最有力的武器之一，它不仅能够梳理业务逻辑，而且与数据库模型设计直接相关。一个好的领域模型能够使您在设计、编码阶段事半功倍。

构建领域模型

还记得在使用UML工具进行业务分析一文中的典例——早期预定旅馆业务Asg_RH，本例将会对此业务中主要的用例进行领域建模。

先回顾一下用例模型，

对应文档中的Task2，我们对其中主要的4个用例Get a list of specified hotels，Choose a hotel，Submit a reservation request to shopping basket和Pay for the reservations in the shopping basket by credit cards进行领域建模。

构建E-R模型

根据领域模型，构建E-R模型就相当容易了。数据库模式设计是一个令人头大的问题，尤其是需求频繁更改的时候，更改数据库表的模式往往牵一发而动全身。良好的领域建模，能够规避一部分此类问题。

如下是根据上述领域模型，使用MySQL Workbench建立的E-R模型，

E-R模型与数据库之间相关，您可以直接由E-R模型生成本例中对应的SQL语句，实现领域模型-ER模型-SQL代码的流水线。

比较

领域模型和E-R模型是完全不同的两回事，领域模型是高层次的模型，具有许多功能；E-R模型重点关注具体的数据库模式。除了进行数据库模式设计，您还可以通过领域模型来

• 梳理业务逻辑
• 驱动开发
• 解释用例
• …

这些都是数据库逻辑模型无法做到的。

在这篇博客中，您将会看到如何使用百度AI开放平台的语音识别技术和UNIT理解与交互技术，实现一个语音控制智能家居的范例。

准备工作

注册百度账号

申请应用

欲使用百度开放平台的API，要先申请应用，获得API KEY才能通过百度API的鉴权。

在控制台的应用列表中点击创建应用，选择所需接口。

本例中需要的接口为百度语音的语音识别以及UNIT两类。

获取Token

在使用百度API前，必须持有百度鉴权发放的Token。获取Token的API如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

### OAuth [GET https://openapi.baidu.com/oauth/2.0/token]

+ Parameters

    - grant_type : `client_credentials` (string, required) - 固定值
    - client_id : `Va5yQRHl********LT0vuXV4` (string, required) - API Key
    - client_secret : `0rDSjzQ20XUj5i********PQSzr5pVw2` (string, required) - API Secret Key

+ Response (application/json)

        {
            "access_token":"1.a6b7dbd428f731035f771b8d********.86400.1292922000-2346678-124328",
            "expires_in":86400,
            "refresh_token":"2.385d55f8615fdfd9edb7c4b********.604800.1293440400-2346678-124328",
            "scope":"public",
            "session_key":"ANXxSNjwQDugf8615Onqeik********CdlLxn",
            "session_secret":"248APxvxjCZ0VEC********aK4oZExMB",
        }

使用百度语音识别

百度语音识别就是将声音文件转化成一段文本，通过调用百度语音提供的REST API完成。如下是一段百度语音识别的API Blueprint（上传文件方式）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

### Baidu ASR [POST http://vop.baidu.com/server_api]

+ Parameters

    - cuid : `d0:a6:37:ed:3d:eb` (string, required) - 用户唯一标识符
    - token : `1.a6b7dbd428f731035f771b8d********.86400.1292922000-2346678-124328` (string, required) - 用户认证Token
    - dev_pid : `1537` (int) - 识别码
    - lan : `zh` (string, deprecated) - 历史兼容参数

+ Request (audio/pcm;rate=16000)

+ Response (application/json)

        {
            "err_no":0,
            "err_msg":"success.",
            "corpus_no":"15984125203285346378",
            "sn":"481D633F-73BA-726F-49EF-8659ACCC2F3D",
            "result":["北京天气"]
        }

关于识别码，指定了识别的语言和方式。

关于请求内容类型，百度语音仅支持3种音频格式：pcm, wav和amr，推荐采样率为16000，推荐编码为16位单声道。

使用百度理解与交互技术UNIT——快速上手

UNIT（Understanding and Interaction Technology），是百度推出的一套完整的人机智能交互解决方案，理解用户语义并执行相应的操作只是其简单的一个小功能。

您可以将UNIT理解成一个机器人，通过对“任务”的定义和数据的训练，使其具备理解和交互的能力。登陆百度账号后，访问UNIT主页进行配置。

场景

一个场景对应一个独立完整的对话系统，通常按垂类划分（例如，天气场景、电视遥控器场景等）。
场景中包含了一系列对话单元用于完成该场景下的所有对话任务（例如，查温度、换台等）。

场景可以理解为一个智能的可交互对象，新建场景是配置UNIT的第一步，本例中，我们新建一个场景叫做“智能家居控制台”

技能

场景中的某个方向的能力。 技能中包含了一系列对话单元或问答单元用于完成该场景下的所有对话任务(例如，智能电视产品包含了换台、调音量、找部电影等一系列对话单元)。

技能相当于场景所具备的能力，目前UNIT仅允许用户自定义一个技能，并添加其预置技能。预制技能也暂时仅有两种：“问候”和“电视指令”。

对话单元

对话单元代表着产品能够执行的某个特定任务（例如，换到中央台）。

对话单元是UNIT执行任务不可再分的要素了，一个对话单元对应一个具体的任务或操作，对话单元是我们工作面对的主要对象。

一个对话单元包含意图、词槽、和答复三个部分，意图实际上就是一个标识符，标识这个任务，解析意图实际上就是正确识别出一个标识符；词槽可以理解为执行这个意图必须的信息，例如“打开灯”这个意图中，打开灯的位置就是一个词槽，用户必须提供能够表示位置的词（例如“客厅”）插入词槽中，这个意图才可以被成功执行；答复就是意图执行的结果，答复可以是“直接回复”，也可以是“引导”，直接回复或回复一段文本，或执行一条函数，而引导则是开启另一个对话单元。

点击自定义技能中的新建单元，即可配置一条新单元。

训练

所有自定义的对话单元都必须经过训练才能保证可用性和准确性，用于训练的最主要手段是样本集，即包含提问和回答的有监督数据。在数据中心中，配置默认集，

然后在训练与验证中就能训练并生效模型，一个模型是当前对话单元、训练集的一个快照，模型必须经过训练并生效到沙盒中才能供测试和API调用。

通用流程

综上所述，场景是训练的基本单位，得到一个智能交互机器人的通用流程如下：

1. 新建一个场景。
2. 定义场景技能。
3. 编制样本集，录入数据中心。
4. 训练。
5. 生效，测试，整合进产品，上线…。

REST API

将模型应用到沙盒中去后，就可以通过REST API访问我们训练好的机器人了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123

### Unit Utterance [POST https://aip.baidubce.com/rpc/2.0/solution/v1/unit_utterance]

+ Parameters

    - access_token : `1.a6b7dbd428f731035f771b8d********.86400.1292922000-2346678-124328` (string, required) - Token

+ Request (application/json)

        {
            "scene_id":123,
            "query":"今天北京天气怎么样?",
            "session_id":""
        }

+ Response (application/json)

        {
            "log_id": 1234,
            "result": {
                "session_id": "xxx",
                "action_list": [
                    {
                        "confidence": 205,
                        "action_id": "aaa",
                        "main_exe": "xxx",
                        "arg_list": [
                            "string",
                            "string"
                        ],
                        "exe_status": [],
                        "say": "xxx",
                        "hint_list": [
                            {
                                "hint_query": "11111"
                            },
                            {
                                "hint_query": "2222222"
                            }
                        ],
                        "action_type": {
                            "act_type": "clarify",
                            "act_target": "slot",
                            "act_target_detail": "loc",
                            "act_type_detail": ""
                        },
                        "code_actions": {}
                    }
                ],
                "schema": {
                    "current_qu_intent": "xxx",
                    "intent_confidence": 3,
                    "bot_merged_slots": [
                        {
                            "begin": 10,
                            "length": 15,
                            "original_word": "word",
                            "normalized_word": "word",
                            "word_type": "string",
                            "type": "XXX",
                            "confidence": 2,
                            "session_offset": 0,
                            "merge_method": "add"
                        }
                    ]
                },
                "qu_res": {
                    "intent_candidates": [
                        {
                            "extra_info": null,
                            "func_slot": "",
                            "intent": "SYS_WEATHER",
                            "intent_confidence": 99.999938964844,
                            "intent_need_clarify": false,
                            "from_who": "",
                            "match_info": "",
                            "slots": [
                                {
                                    "confidence": 99.99959564209,
                                    "length": 4,
                                    "normalized_word": "2017-05-25",
                                    "offset": 0,
                                    "original_word": "今天",
                                    "type": "sys_time",
                                    "word_type": "",
                                    "need_clarify ": true
                                }
                            ]
                        }
                    ],
                    "lexical_analysis": [
                        {
                            "basic_word": [
                                "中国"
                            ],
                            "type": "21",
                            "term": "中国",
                            "weight": 0.1911181211471558
                        },
                        {
                            "basic_word": [
                                "北京"
                            ],
                            "type": "6",
                            "term": "北京",
                            "weight": 0.3822362422943115
                        },
                        {
                            "basic_word": [
                                "人民",
                                "大学"
                            ],
                            "type": "7",
                            "term": "人民大学",
                            "weight": 0.4266456961631775
                        }
                    ],
                    "sentiment_analysis": {
                        "label": 2,
                        "pval": 0.196025
                    }
                }
            }
        }

返回的数据量非常大，关于这部分您可以查看百度官方技术文档，在这里不做赘述。

实践

UNIT测试

本例定义了一个简单的“开灯”对话单元，有一个“位置”词槽，使用3个样本数据训练了一个迷你机器人。

在百度UNIT页面可与训练好的BOT进行交互：

当然，实战需要更加海量的数据。

语言实践

本例使用Go语言编写了一个百度AI客户端包，目前可以做到：

• 获取并管理Token；
• 语音识别；
• 访问UNIT机器人。

测试代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

package main

import (
	"fmt"

	"github.com/hinanawitenshi/baiduai"
)

func main() {
	c := baiduai.NewClient(
		"myapikey",
		"mysecretkey",
	)
	c.NewSession()
	fmt.Println(c.Voice2Text("audio.wav", "wav", "16000", 1536))
	fmt.Println(c.Unit(20079, "打开客厅灯", 1))
}

返回结果：

1
2

&{0 success. 842193954671523782416 6544595644287405787 [明天天气怎么样]}
&{152378241880814 0  {1 [{turn_light_on_satisfy {   } [] {} 1 []  OK []}] {TURN_LIGHT_ON 99.99630737304688 [{0 0 0 客厅  user_location 0 update}]} {[] [] {0 0}}}}